환웅 데이터
[STAT155] Chapter 1: Combinatorial games 본문
1. 조합론적 게임 정의 (Combinatorial Games)
조합론적 게임에서는 두 명의 플레이어, 위치들의 집합, 그리고 위치 간 이동할 수 있는 합법적 이동(legal moves)이 정의됩니다. 플레이어들은 한 위치에서 다른 위치로 이동하며 번갈아가며 게임을 진행합니다.
터미널 위치(terminal position): 특정한 위치에서 더 이상 이동할 수 없는 상태.
터미널 위치는 플레이어 I 또는 플레이어 II 중 누가 이겼는지에 따라 win과 lose가 label됩니다.
이 챕터에서는 유한한 단계(finite number of steps) 안에서 종료되는 조합론적 게임에 초점을 맞춥니다.
Example 1.0.1 (Chomp)

Chomp는 초콜릿 바를 사용하는 두 명의 플레이어 게임입니다.
초콜릿 바는 정사각형 칸으로 나뉘어 있으며, 왼쪽 아래 모서리 칸(bottom left corner)은 제거된 뒤 브로콜리로 대체됩니다.
각 턴에 플레이어는 아직 먹히지 않은 초콜릿 칸 하나를 선택합니다.
선택한 초콜릿 칸과 그 칸의 오른쪽 위에 있는 모든 칸을 제거하는겁니다.
마지막 초콜릿 칸을 제거하는 사람이 승자, 초콜릿이 남지 않고, 남은 브로콜리를 먹어야 하는 사람이 패자가 됩니다.
그림 1.1에서는 Chomp 게임의 두 차례 이동을 보여줍니다.
Chomp 예시에 대해서는 Example 1.1.6에서 다시 자세히 설명한다고 하네요~
Definition 1.0.2: 유한한 단계에서 종료되는 게임
▶A combinatorial game with a position set X is said to be progressively bounded if, for every starting position x ∈ X, there is a finitie bound on the number of moves until the game terminates.
위치 집합 X를 가진 조합론적 게임은 다음과 같은 경우 점진적으로 제한(progressively bounded)되었다고 합니다:
X의 모든 시작 위치 x에 대해, 게임이 종료될 때까지의 이동 횟수가 유한하다.
x에서 터미널 위치로 이동하는 데 필요한 최대 이동 횟수를 B(x)로 정의합니다.
조합론적 게임의 두 가지 유형
조합론적 게임은 일반적으로 두 가지 유형으로 나뉩니다:
Impartial Games (공정한 게임):
승리 조건과 가능한 이동이 두 플레이어에게 동일합니다.
▶Winning positions and the available moves are the same for both players.
예시: Nim 게임
첫 번째로 terminal position에 도달하는 플레이어가 승리합니다.
Partisan Games (편파적 게임):
두 플레이어가 서로 다른 승리 조건과 이동 가능성을 가집니다.
이러한 편파적 게임에서는 각 플레이어가 다른 이동 가능성과 승리 조건을 가지며, 플레이어마다 전략이 다르게 형성됩니다.
★체스와 같은 몇몇의 partisan game들은 무승부로 승부가 끝날 수 있지만, 해당 수업에선 이런 경우를 다르지 않을 겁니다.
주어진 조합론적 게임에서 우리의 목표는 특정 플레이어가 항상 승리를 보장할 수 있는지를 확인하는 것입니다. 만약 그렇다면, 승리 전략(winning strategy)을 찾아야 합니다. 즉, 해당 플레이어가 어떤 상황에서도 어떤 수를 두어야 승리할 수 있는지를 결정합니다. 유한 단계에서 종료되는 공정한 게임에서는 무승부가 없으며, 두 플레이어 중 한 명이 반드시 승리 전략을 가질 수 있습니다.
1.1 공정한 게임 (Impartial Games): Subtraction 예제
Example 1.1.1: Subtraction (뺄셈 게임)
규칙:
x∈N개의 칩이 쌓여 있다고(pile of chips) 가정하고, 두 플레이어가 번갈아가며 1~4개의 칩을 가져갑니다. 마지막 칩을 가져가는 플레이어가 승리합니다.
▶시작 칩 수가 4 이하일 경우, 첫 번째 플레이어는 모든 칩을 가져가서 승리합니다.
▶ 시작 칩 수가 5일 경우, 첫 번째 플레이어는 1~4개의 칩을 가져가게 되는데, 두 번째 플레이어는 남은 칩 수에 따라 남은 1~4개의 칩을 모두 가져가며 승리합니다.
▶ 시작 칩 수가 6~9일 경우, 첫 번째 플레이어가 적절히 칩을 가져가 두 번째 플레이어를 패배로 몰아넣습니다.
▶ 10개의 칩이 주어지면, 두 번째 플레이어가 항상 승리 전략을 가질 수 있습니다.
승리와 패배를 정의하기 위한 집합:

N: 첫 번째(next) 플레이어가 승리를 보장할 수 있는 칩 수의 집합.
P: 두 번째(previous) 플레이어가 승리를 보장할 수 있는 칩 수의 집합.
다시 말해,
N에는 {1,2,3,4,6,7,8,9}가 올 수 있고 P는 {0,5}가 올 수 있다는 걸 확인했는데, 계속하자면
P = {x ∈ 전체실수N : 5로 나누어떨어지는 x}이고, N = 전체실수N∖P(차집합)가 됩니다.
결론적으로 첫 번째 플레이어는 x∈N일 때만 승리를 보장하며, x∈P일 때는 두 번째 플레이어가 승리합니다.
Definition 1.1.2 공정한 조합론적 게임(impartial combinatorial game) 정의
공정한 조합론적 게임은 두 플레이어(2 players)와 가능한 위치 집합(set of possible positions)으로 구성됩니다.
플레이어는 한 위치에서 다른 위치로 이동(move)하면서 게임을 진행합니다.
터미널 위치(terminal position): 더 이상 이동이 불가능한 위치입니다.
모든 비터미널 위치(non-terminal position)는 동일한 이동 규칙이 적용(set of legal moves)되며, 이는 두 플레이어 모두에게 동일합니다.
graph (그래프 표현)
node와 link의 집합체로 표현된걸 graph라고 부릅니다.
게임 위치(game positions): 노드(node)로 표현됩니다.
이동(moves): 방향 있는 링크(directed link)로 표현됩니다.게임 시작 시, 토큰(token)은 초기 위치(initial position)를 나타내는 노드에 놓이며, 플레이어들은 링크를 따라 이동하면서 terminal node에 도달합니다.
해당 정의로 알 수 있는 사실은, Subtraction 게임은 공정한 게임(impartial game)이란 겁니다.
유일한 터미널 위치는 x=0입니다. 그림 1.2는 초기 위치 x=14에서의 Subtraction 게임 그래프를 보여줍니다.
starting position x∈N에서, 다음 플레이어는 항상 P에 속하는 위치로 이동함으로써 승리를 보장할 수 있습니다.
예시: P = {5n : n ∈ 전체실수N}.
Definition 1.1.3
플레이어의 전략(strategy)은 각 비종료 상태(nonterminal position)에 대해 합법적인 움직임(legal move)을 할당하는 함수입니다. 특정 위치 x에서의 승리 전략(winning strategy) 은 해당 위치 x에서 시작하여 유한한 단계 내에 플레이어가 반드시 승리할 수 있도록 보장하는 전략을 의미합니다.
그림 1.2
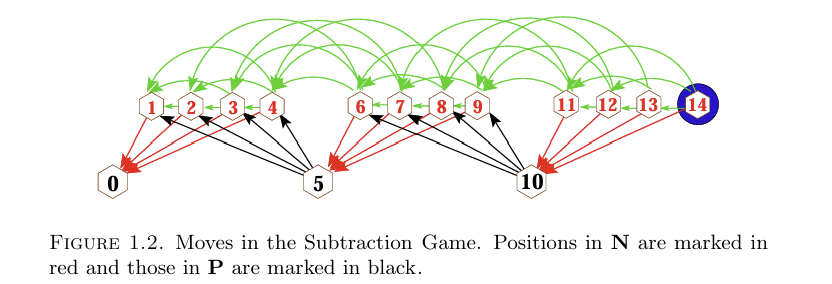
서브트랙션 게임(Subtraction Game)의 이동을 나타낸 그림입니다. 빨간색으로 표시된 위치는 N이고, 검은색으로 표시된 위치는 P입니다.
특정 x에서 승리를 보장하는 전략은 유한한 단계 내에서 플레이어가 이길 수 있도록 보장합니다. 우리는 N과 P의 개념을 모든 공평한 게임(impartial game)으로 확장할 수 있습니다.
Definition 1.1.4
어떤 공평한 조합 게임(impartial combinatorial game)에 대해, N (next의 약자)을 첫 번째로 움직이는 플레이어가 승리를 보장할 수 있는 위치 집합으로 정의합니다. 모든 움직임이 N-위치로 이어지는 위치 집합은 P (previous의 약자)로 나타냅니다. P-위치를 강제할 수 있는 플레이어는 승리를 보장할 수 있습니다.

집합 Ni와 Pi는 재귀적으로 정의될 수 있습니다.


Definition 1.1.5
점진적으로 제한된 공평한 조합 게임에서, 일반적인 게임 규칙(normal play)1 하에서는 모든 위치가 N 또는 P (N∪P)에 속합니다. 따라서, 어떤 초기 위치에서든 한 플레이어는 반드시 승리 전략을 가집니다.
증명
B(x)는 위치 x에서 종료 위치까지의 최대 이동 횟수라고 정의합니다. 귀납법을 통해 B(x)≤n인 모든 위치 x가 Nn 또는 Pn (Nn∪Pn) 에 속한다는 것을 증명합니다.
1. 모든 위치는 N∪P에 속함
N (Next-position): 현재 플레이어가 승리를 보장할 수 있는 위치
P (Previous-position): 상대 플레이어가 승리를 보장할 수 있는 위치
귀납적 가정을 이용하여, 모든 위치는 N 또는 P에 포함됨을 증명함.
Chomp 게임 개요 (Example 1.1.6)
Chomp는 초콜릿 바를 잘라가면서 진행하는 게임으로, 특정한 규칙에 따라 조각을 먹어야 함.
이 게임이 Progressively Bounded되어 있음을 언급하며, 정리 1.1.5를 적용하면 어느 한쪽이 반드시 이기는 전략을 가질 수 있음을 보장함.
이기는 전략이 첫 번째 플레이어에게 있음을 증명하고자 합니다.
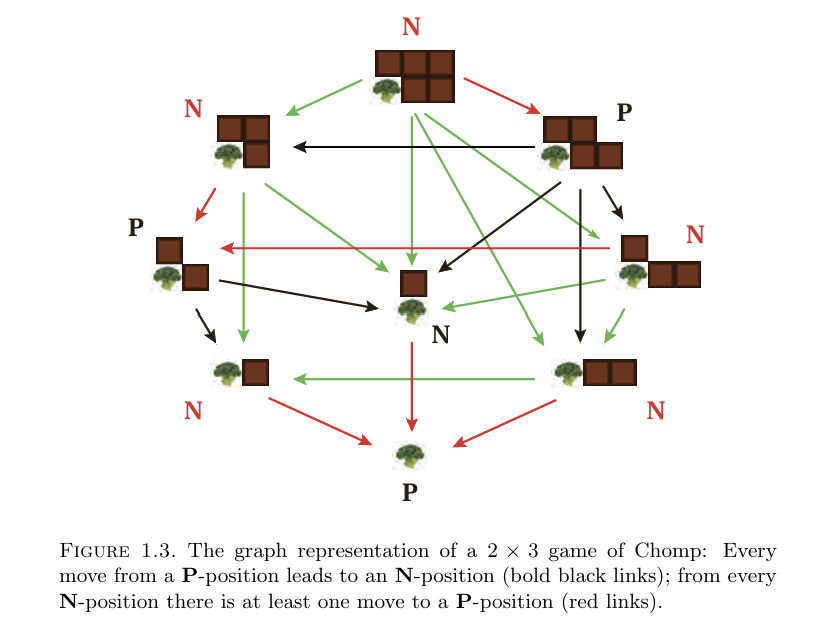
Chomp 게임의 그래프 표현 (그림 1.3)
P-위치에서의 움직임은 N-위치로 이어짐 (굵은 검은색 선).
N-위치에서의 움직임은 반드시 하나 이상의 P-위치로 이어짐 (빨간색 선).
이를 통해 특정 위치가 승리 전략을 가질 수 있는지 시각적으로 표현함.
Theorem 1.1.7 – Chomp 게임에서 승리 전략 증명
초콜릿 바가 1×1보다 클 때, 다음 플레이어가 승리 전략을 가짐.
귀납적으로 증명:
초콜릿 바 R에서 오른쪽 상단 1×1 조각을 제거한 R −를 생각.
만약 R−가 P-위치라면, R은 N-위치가 됨 → 오른쪽 상단을 먹는 것이 이기는 전략.
만약 R −가 N-위치라면, R −에서 P-위치로 가는 이동이 존재하므로, R도 결국 N-위치가 됨.
이 증명을 통해 Chomp 게임에서는 첫 번째 플레이어가 무조건 이기는 전략을 가질 수 있음을 보장함.
1. 전략 도둑질(Strategy-stealing)
증명에서 사용된 기법을 전략 도둑질(strategy-stealing)이라 부릅니다. 하지만 이 기법은 구체적인 이기는 전략을 제공하지는 않아요. 단지 첫 번째 플레이어에게 이기는 전략이 반드시 존재함을 증명하는 역할만 수행합니다.
1.1.1 Nim 게임 분석
Nim 게임은 여러 개의 말뚝(piles)이 있고, 각 말뚝에는 유한한 개수의 칩(chips)이 있음.
플레이어는 한 말뚝에서 원하는 개수의 칩을 제거할 수 있으며, 마지막 칩을 제거하는 사람이 승리.
종료 위치(terminal position): 모든 칩이 사라진 상태.
이 게임은 Progressively Bounded하므로, 모든 위치는 N (이기는 위치) 또는 P (지는 위치)에 속함.
게임 위치 분석
위치를 (𝑛1,𝑛2,…,𝑛𝑘)로 표시: k개의 말뚝이 있으며, 각각의 말뚝에 𝑛1,𝑛2,…,𝑛𝑘개의 칩이 있음.
초기 분석:
(0,1)과 (1,0)은 N (이기는 위치)
(1,1)은 P (지는 위치) → 가능한 두 가지 이동이 (0,1) 또는 (1,0)인데, 둘 다 N에 속하므로 상대방이 승리할 수 있음.
(1,2), (2,1)은 N → 다음 플레이어가 (1,1)로 이동 가능하므로 승리 전략이 존재함.
(n,n)은 항상 P (지는 위치)
(n,m) (단, n<m)는 N (이기는 위치) → 큰 말뚝에서 m−n 개의 칩을 제거하면, 상대방이 (n,n) (지는 위치)로 가게 됨.
말뚝이 3개일 때 분석:
(1,2,3)은 P (지는 위치)
첫 번째 플레이어가 어떤 수를 제거하더라도 상대가 두 개의 말뚝을 같은 크기로 맞출 수 있음 → 상대방이 승리 전략을 가짐.
(1,2,3,4)는 N → 다음 플레이어가 4번째 말뚝을 제거하여 (1,2,3)으로 만들 수 있음.
5. 보조정리 (Lemma 1.1.9)
두 개의 Nim 위치 X 와 Y가 주어질 때:
X,Y가 둘 다 P이면 (X,Y)도 P.
X가 P이고 Y가 N (또는 그 반대)이면 (X,Y)는 N.

그림 1.4 설명
그림에서 (n, m) (단, n<m)은 N에 속함.
플레이어의 최적 전략은 더 큰 말뚝에서 m−n 개의 칩을 제거하여 (n, n) 상태로 만드는 것.
(n, n)은 지는 위치이므로, 상대방이 결국 패배하게 됨.
'Game Theory STAT155' 카테고리의 다른 글
| [STAT155] Rim Game 정리 (0) | 2025.03.03 |
|---|---|
| [STAT155] Chomp Game 정리 (0) | 2025.02.27 |
| [STAT155] Nim Game 정리 (0) | 2025.02.05 |