STAT134 Lec21

Section 4.2 E(X) and Var(X) of Exp(λ) (지수 분포의 평균과 분산)

 

Gamma Distribution (감마 분포)

감마분포 a개의 사건(포아성 사건이 a회 발생)이 일어날 때까지 걸리는 대기 시간에 대한 분포이다. 지수 분포는 a = 1일때의 감마 분포라고 할 수 있다. 평균사건발생 횟수인 람다는 일정해야한다.

포아송 분포는 람다를 모수로 가지고, 단위 시간과 단위 공간에서 어떤 사건이 몇번 발생할 것인지를 나타내는 분포이다.

다시 한번, 포아송 분포는 어떤 단위 구간(시간)에서 일어나는 특정 사건의 발생 횟수에 대한 분포이다.

특정 시간동안 톨게이트에 도착하는 차량의 개수를 예시로 들 수 있다. 또 예를 들어, 포아송 분포를 통해서 평균발생횟수가 5개 되는 단위 구간에서 사건이 3개 일어날 확률은 구할 수 있지만, 그 구간 내에서 사건은 랜덤으로 일어나기에 정확한 타이밍은 예측할 수 없다. 사건이 무작위가 아닌 어떠한 규칙에 의거하여 발생한다면 그것은 포아송 분포가 아니다. 

평균은 λt 와 같다.

 

예시 문제를 살펴보자.

밑에 나오는 감마 함수는 Γ(r) = (r - 1)! , r = 1, 2, 3, . . .

자, Tr은 r번째 성공까지 걸린 시간이다. Nt는 t 시점까지의 성공 횟수이다. t 시점 이후에 r번째 성공이기 위해서는, t 시점 이전에서 r-1번째 성공이 존재해야한다. 

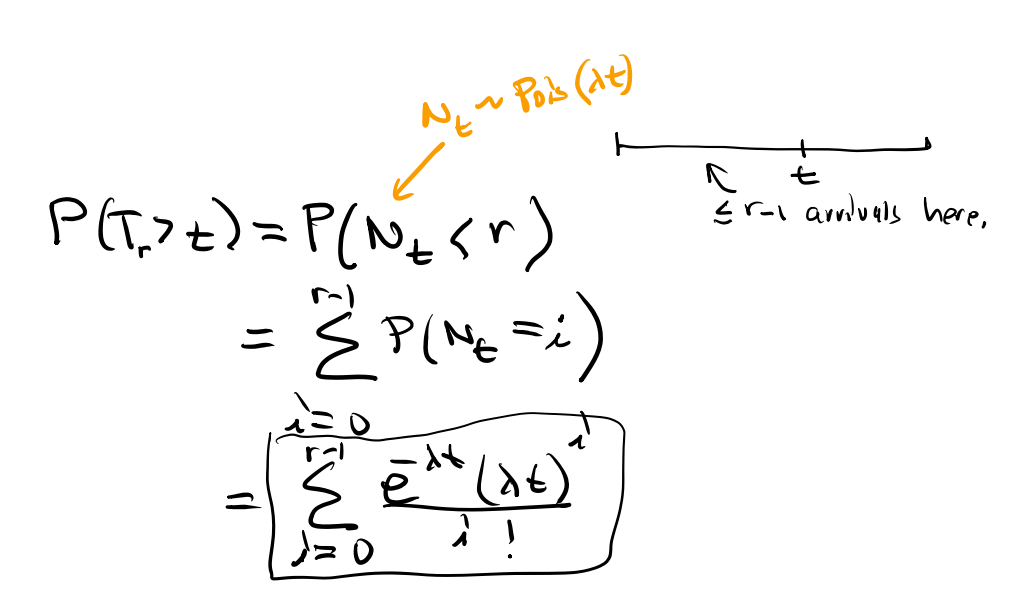
어렵다..어려워. 감마 분포와 포아송 분포의 관계를 보이고 있다. 직관적으로 이해하지 못하고 있다.

예시 문제를 살펴보자. 다시, Tr은 r번째 성공까지 걸린 시간이다. Nt는 t 시점까지의 성공 횟수이다.

평균은 λt (2 * 7)와 같다.

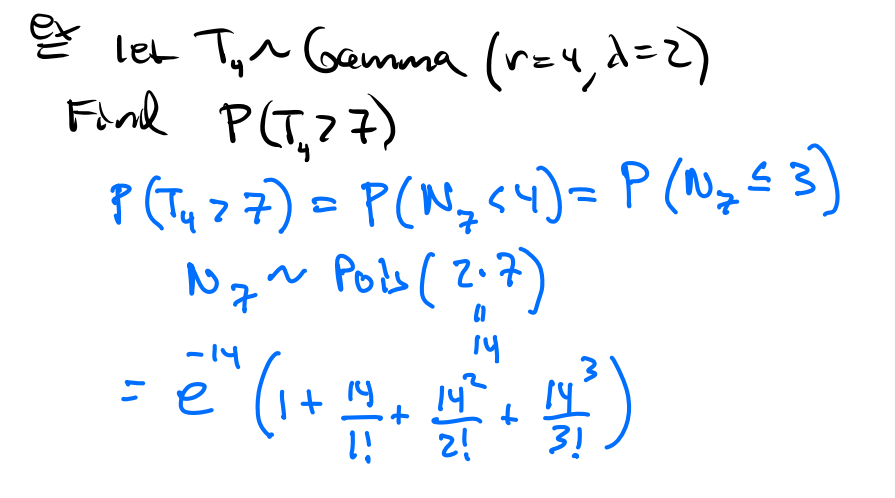
또다른 예시 문제 이다.

Gamma function 감마 함수

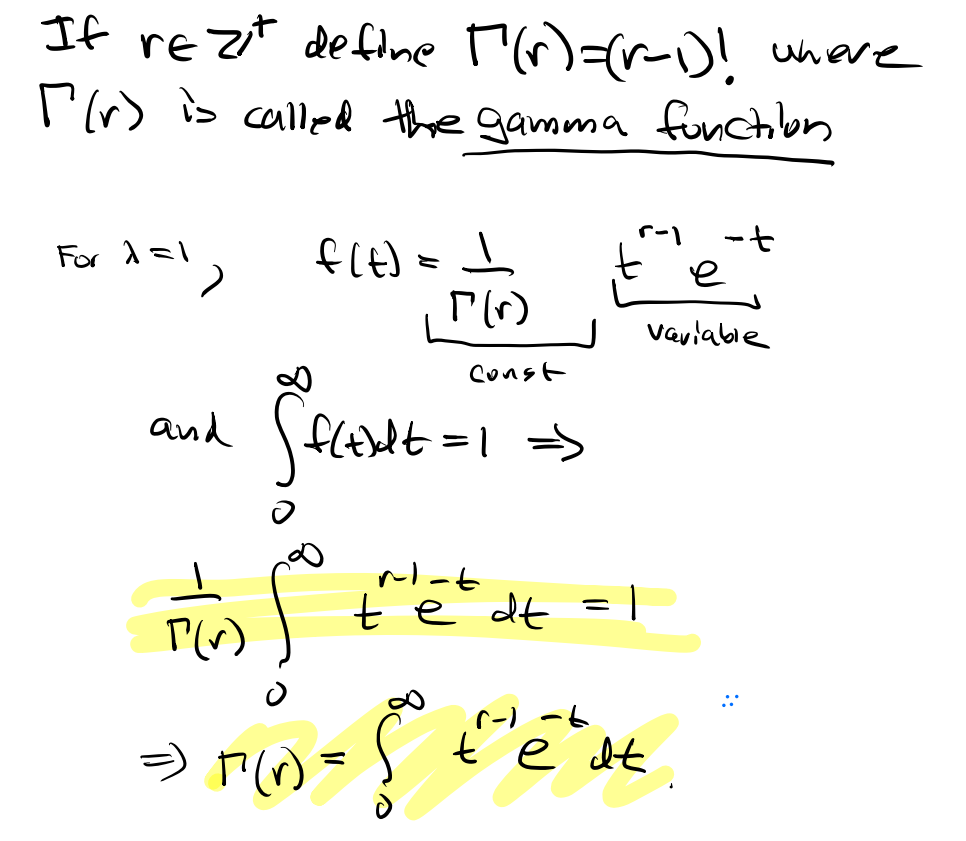
예시를 살펴보자.

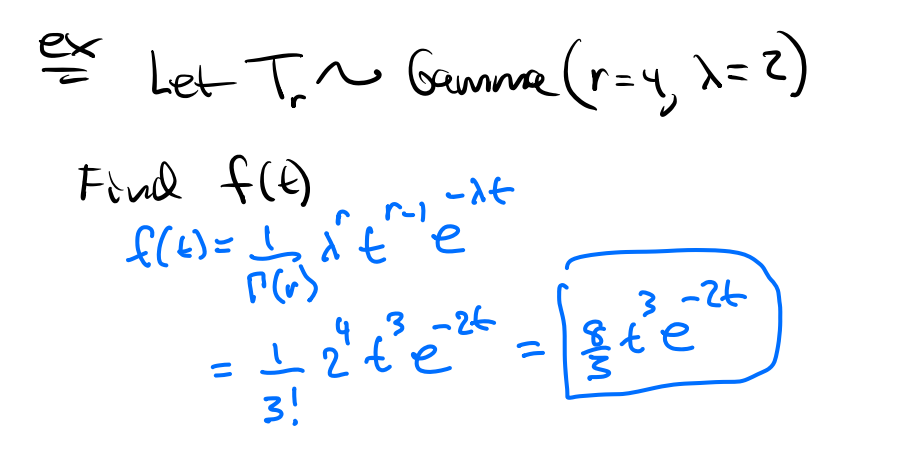
지수 분포의 평균과 분산 증명

 

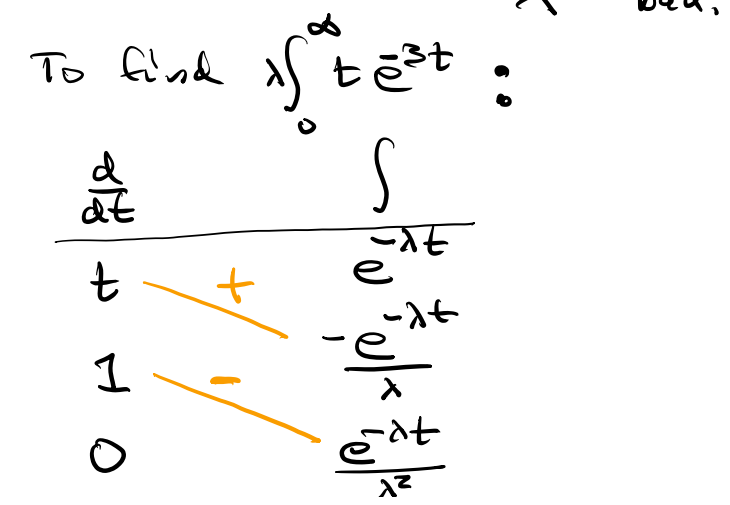
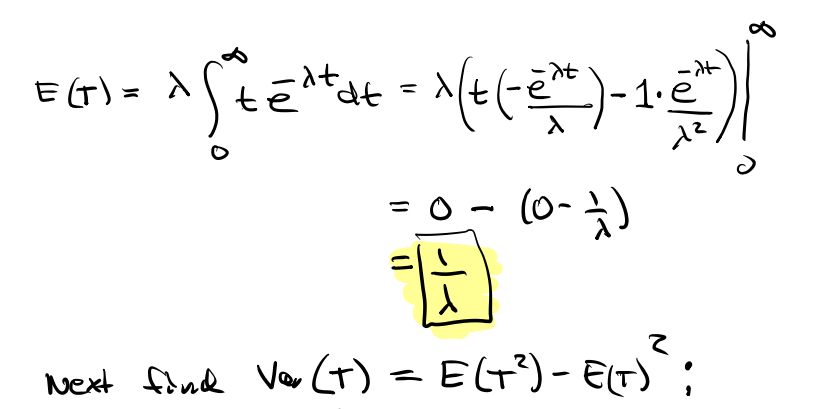
Works Cited:

https://soohee410.github.io/discrete_dist3

[이산형 분포] 포아송 분포(Poisson distribution)

https://dogmas.tistory.com/entry/%ED%99%95%EB%A5%A0%EC%9D%B4%EB%A1%A0-%EC%A0%95%EB%A6%AC9-%EA%B0%90%EB%A7%88-%EB%B6%84%ED%8F%ACGamma-Distribution

확률이론 정리9. 감마 분포(Gamma Distribution)

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=gdpresent&logNo=221138171419 

감마분포(Gamma Distribution) 유도 [ 내가 공부한 통계학 기초 #4 ]