환웅 데이터
Python[CS61A] Functions: Textbook (1.1~1.7) 정리 본문
Python[CS61A] Functions: Textbook (1.1~1.7) 정리
환 웅 2024. 10. 4. 18:45Ch. 1.1
1.1.3 Interactive Sessions
Interactive session에서는, 프롬프트의 '>>>' 문자 뒤에 Python 코드를 작성할 수 있다. Prompt(>>>)가 보이면, Python Interactive Session이 시작되었다고 할 수 있다. 그러면 Python 인터프리터가 입력된 코드를 읽고 실행한다.
Interactive controls: 각 session들은 사용자가 타이핑한 내용들을 히스토리로 저장하고 있는데,
이 히스토리에 대한 접근법은 다음과 같다.
Ctrl + P (previous, 이전)
Ctrl + N (next, 다음)
Ctrl + D (discard, 끝내기)
ㄴdiscard 사용시 히스토리가 사라진다.
1.1.4 First Example
>>> from urllib.request import urlopen
import 구문은 인터넷을 사용하여 데이터에 접근하는 기능들을 로드하는 작업을 한다.
urlopen 함수는 Unified Resource Indicator(URL)을 통해 인터넷 콘텐츠에 접근할 수 있는 라이브러리다.
Statements & Expressions
파이썬 코드는 식(expression)과 구문(statement)으로 구성된다.
- Expressions don't have to involve an operator
- A number by itself is an expression
컴퓨터 프로그램은 명령어들로 구성되는데, 이 명령어들은 다음 두 목적을 보통 가진다.
- Compute some value
- Carry out some action
Interpreter가 statement를 실행한다는 것은, 그에 상응하는 작업을 수행한다는 의미를 가진다.
파이썬이 expression을 evaluate한다는 것은 그 식의 값을 계산한다는 의미를 가진다.
즉 evaluation이라는 표현은, expression을 결과(value)로 바꾸어주는 동작을 의미한다.
예를 들어, 4 + 3이라는 expression을 7로 처리하는걸 evaluation이라고 한다.
구문(statement)은 일반적으로 single line code나 code block을 의마한다.
일반적으로 하나 이상의 expression으로 구성되어 있다.
즉, 모든 expression은 statement이다. 더 포괄적인 개념이라고 할 수 있겠다.
하지만, 모든 statement는 expression이 아니다.
할당문(Assignment statement)
>>> shakespeare = urlopen('http://composingprograms.com/shakespear.txt')shakespear에 '='를 통해서 expression의 값을 부여했다.
URL문자열에 urlopen 함수를 사용해서 하나의 완전한 텍스트 문서를 가져오는 코드이다.
>>> words = set(shakespeare.read().decode().split())words라는 이름 안에, set of all unique words that appear in Shakespeare's plays를 전부 넣어준다.
read(), decode(), split()은 (역주:method chain)로서 각각 중간 연산(intermediate computational entity)을 수행한다.
이 코드를 통해 우리는 열린 URL을 통해서 데이터를 읽고(read), 데이터를 텍스트로 변환(decode)하고, 텍스트를 단어로 자른다(split). 이 단어들을 모두 set에 넣었다.
함수(Functions)
함수란 데이터를 다루는 logic을 캡슐화(encapsulation)하는 존재다. 위 할당문에서 봤던 urlopen이 바로 함수다. 함수의 세부 프로세스는 복잡하겠지만, 이 복잡함이 함수 안에(위에선 urlopen 안에) 숨겨져 있기(tucked away) 때문에 우리는 간단한 expression만으로 작업 수행이 가능하다.
객체(Object)
set은 object의 일종(type)으로, 교집합을 구하거나 원소들의 개수를 알려주는 연산을 지원한다. Object는 데이터와 그 데이터를 다루는 logic을 매끄럽게 묶어주어서 복잡성을 관리할 수 있게 만들어주는 역할을 한다.
>>> {w for w in words if len(w) == 6 and w[::-1] in words}이는 합성식(compound expression)으로 불린다. 해당 식은 Shakespearian 단어들의 set에서 거꾸로 해도 똑같은 단어들을 찾아내는 식이다. w[::-1]은 단어를 구성하고 있는 각각의 문자(letter)를 열거(enumerate)하는 로직인데, -1은 reverse 방향을 의미한다.
인터프리터(Interpreters)
파이썬 코드를 번역해주는 프로그램이다.
파이썬 코드를 작성할 때 컴퓨터가 바로 이해할 수 있는게 아님. 컴퓨터가 이해 가능한건 오로지 machine code이고, 이 파이썬 코드를 machine code로 번역해주는 프로그램이 interpreter.
교재의 설명을 빌리면, 코드를 예측가능한 방법으로 해석하는 정확한 절차를 구현해서 합성식(compound expressions)를 평가하는 프로그램을 인터프리터로 정의한다.
결국엔 이런 핵심 개념들이 밀접하게 관련이 되어 있는데, 함수는 객체이고 객체는 함수이다. 그리고 인터프리터는 객체와 함수를 모두 포함하는 인스턴스(instance)이다. >> 이해를 못하겠다.
Ch. 1.2
1. 원시적 표현과 구문(primitive expressions and statements)
- 언어가 제공하는 가장 간단한 단위(simplest building block)
2. 조합 방법(means of combination)
- 어떻게 단순한 것에서 복잡한 것(compound element)을 만드는지
3. 추상화 방법(means of abstraction)
- 만들어진 복잡한 것이 어떻게 이름지어지고 단위화되는지
1.2.1 표현식(Expressions)
숫자(number)는 primitive expression의 한 종류이다. 우리가 타이핑하는 숫자는 10진수(number in base10)를 말한다.
Primitive expressions의 종류: number or numeral, name, and string
주의: 파이썬에서는 모든 데이터 타입이 객체(object)고, primitive data type은 존재하지 않는다
>>> 42
42숫자 표현식은 수학 연산자로 결합되어 합성식(compound expression)이 될 수 있다. 이 합성식은 interpreter가 평가할 것이다.
>>> -1 - -1
0
>>> 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
0.9921875해당 코드는 중위 표기법(infix notation)을 사용하고 있다.
중위 표기법은 우리가 일상적으로 사용하는 수학적 표현 방식이다. 중위 표기법에서는 연산자(+, -, *, /) 들이 피연산자(operand)인 숫자 사이에 들어가게 된다.
1.2.2 호출식(Call Expressions)
가장 중요한 종류의 compund expression은 호출식(call expression)이다. 호출식은 특정 매개변수(argument)에 함수를 적용하라는 명령이다. Algebra에서 input argument가 함수에 mapping되어 output값을 출력하는 과정을 생각해보자. 예를 들어, max()함수는 여러 개의 입력값에 대해서 최대값이라는 하나의 출력값을 리턴한다.
>>> max(7.5, 9.5)
9.5이 호출식은 하위식(subexpression)을 가지고 있다.
여기서 연산자(operator)는 쉼표로 구분된(comma-delemited) 피연산자(operand) 리스트(7.5, 9.5)를 감싸고 있는 괄호 앞의 max이다.
(사진 첨부할 것)
이 operator는 함수(function)를 의미한다. 이 호출식이 평가될 때, 우리는 'max()가 arguments 7.5와 9.5에 대해 호출되어 9.5라는 값을 리턴했다'고 한다. max() is called with arguments 7.5 and 9.5, and returns a value of 9.5.
argument의 순서가 중요한 경우도 있는데, 예를 들어 pow() 함수는 첫번째 argument의 두번째 argument 지수 승한 결과이다. 두 순서를 바꾸면, 아예 다른 표현식이 되는 거겠죠?
>>> pow(100, 2)
10000
>>> pow(2, 100)
1267650600228229401496703205376
함수 표기법(function notation)의 three principal advatanges over the 수학적 표기법인 중위 표기법(mathematical convention of infix notation)
첫 번째, 함수가 임의의 개수의 arguments를 가질 수 있다.
두 번째, 함수 표기법은 그대로 중첩 표현식(nested expression)으로 확장될 수 있다. 중첩 표현식에서는 compund expression들 그 자체도 요소(elements)가 된다. 합성 중위 표현식(compund infix expression)과 달리 nested call expression에서는 중첩 구조가 괄호로 명시 된다. (합성 중위 표현식도 순서를 괄호로 명시하지 않나??)
>>> max(min(1, -2), min(pow(3, 5), -4))
-2세 번째, 다양한 형태를 가지는 수학적 표기법에서 오는 어려움을 호출 표현식을 통해 통합시킴으로써 단순화할 수 있다. 파이썬이 infix notation으로 지원하는 연산자는 모두 함수로 정의되어 있기 때문에 함수명을 통해서 호출이 가능하다.
1.2.3 Importing Library Functions
파이썬의 모든 함수들의 이름이 default로 사용 가능한 것은 아니다. 대신, 사용하려는 함수가 위치한 파이썬 라이브러리를 알고 있다면 사용할 수 있다. 라이브러리를 사용하려면 import를 해야한다. 예를 들어, math 모듈은 우리에게 익숙한 수학적 함수들을 제공한다.
>>> from math import sqrt
>>> sqrt(256)
16.0그리고 operator 모듈은 infix notation에 상응하는 함수들을 제공한다.
>>> from operator import add, sub, mul
>>> add(14, 28)
42
>>> sub(100, mul(7, add(8, 4)))
16import구문은 operator 또는 math 같은 모듈 이름을 가리킨다. 다음으로, 그 모듈에서 가지고 올 속성(sqrt, add등)의 리스트가 온다. 함수를 한 번 import 하고나면, 여러번 호출하는 것이 가능하다.
1.2.4 Names and the Environment
어떤 값에 이름(names)이 주어졌다는걸, 우리는 '값에 이름이 bind 되었다'고 표현한다.
If a value has been given a name, we say that the name binds to the value.
파이썬에서는 할당문을 사용해서 새롭게 binding하는 것이 가능하다. 이름은 =의 왼쪽에, 값은 오른쪽에 온다.
>>> radius = 10
>>> radius
10
>>> 2 * radius
20
이름은 import 구문을 통해서도 bind 될 수 있다. (아래 코드에선 pi가 그 예시겠네요)
>>> from math import pi
>>> pi * 71 / 223
1.0002380197528042
파이썬에서 = 기호는 할당 연산자(assignment operator)라고 불린다. assignment라는 것은 어떤 것을 추상화(abstraction)하는 가장 간단한 방법이다. 예를 들어, 위에서 계산되는 compound operation의 결과는 area라는 이름을 붙임으로써 추상화될 수 있다.
이름을 binding하고 이후에 그 이름을 통해 값을 불러오는 것은 인터프리터가 이름, 값, binding에 대한 정보를 유지하기 위해서 메모리를 사용한다는 의미다. 이런 메모리를 환경(environment)라고 부른다.
또한 이름은 함수에도 bind될 수 있다. 예를 들어, max라는 이름은 우리가 사용했던 max() 함수에 binding된 이름이다. 숫자와 다르게 함수는 텍스트로 표현되기 어렵기 때문에 파이썬은 이 함수의 description을 리턴하게 된다. (description을 리턴한다는게 무슨 뜻일까?)
>>> max
<built-in function max>이렇게 이미 존재하는 함수의 이름을 변경하기 위해 assignment statement를 사용해볼 수 있다.
>>> f = max
f
<built-in function max>
>>> f(2, 3, 4)
4이 이름에 다시 새로운 값을 할당할 수도 있다.
>>> f = 2
>>> f
2파이썬에선 이런 이름을 변수명(variable name)이나 변수(variable)이라고 부른다. 그 이유는, 이름들이 프로그램을 실행하는 과정에서 다른 값들로 binding, 즉 변할 수 있기 때문이다. 만약 어떤 이름이 할당을 통해 새로운 값에 bind 된다면, 이전 값에 대한 binding은 없어지는거다.
>>> max = 5
>>> max
5즉, max에 5를 할당하고 나면 max라는 이름은 더 이상 함수에 binding되지 않기에, max(2, 3, 4)와 같은 호출 시도는 에러를 발생시킬 것이다.
할당문을 실행할 때, 파이썬은 =의 왼쪽에 있는 binding을 바꾸기 전에 오른쪽의 식을 먼저 평가한다. 그러므로 할당문에 의해 이름에 binding이 생겼다면 우변에서 그 이름을 참조할 수 있다. 코드를 보면 더 직관적으로 이해가 가능하다.
>>> x = 2
>>> x = x + 1
>>> x
3또한 하나의 구문에서 여러 개의 값을 여러 개의 이름에 할당하는 것도 가능하다. 이렇게 하려면 좌변에 이름들을 쉼표로 구분해서 기술하고, 우변에 식들을 쉼표로 구분해서 기술해야한다.
>>> area, circumference = pi * radius * radius, 2 * pi * radius
>>> area
314.1592653589793
>>> circumference
62.83185307179586어떤 이름의 값을 바꾸었다고 해서 다른 이름들에게 영향을 바로 주지 않는다. 아래 코드를 보면, area라는 이름은 새로운 값을 binding 받은 radius의 할당문에 영향을 받지 않기 때문에, area의 값도 바꾸고 싶다면 다른 할당문을 사용해야 한다.
>>> radius = 11
>>> area
314.1592653589793
>>> area = pi * radius * radius
380.132711084365다중 할당문(multiple assignment)을 시행할 때는 좌변의 이름들에 값이 할당되기 이전에 우변의 모든 식이 평가된다. 이 규칙 때문에 두 이름의 값을 바꾸는 연산이 하나의 문장에서 수행될 수 있다.
>>> x, y = 3, 4.5
>>> y, x = x, y
>>> x
4.5
>>> y
3
1.2.5 중첩 호출식의 평가 (Evaluating Nested Expressions)
파이썬 인터프리터는 다음과 같은 절차를 따를 것이다.
- 연산자(operator)와 피연산자(operand) 하위식(subexpressions)을 평가한다.
- 연산자의 하위식에서 나온 값에 해당하는 함수를 피연산자 하위식 값의 argument로 적용한다.
직관적인 이해는 어렵네요. 첫번째 단계는 호출식의 평가가 제대로 수행되기 위해서 다른 식들의 평가가 먼저 이루어져야 한다고 말하고 있습니다. 그러므로 평가 절차는 자연스럽게 재귀(recursice) 되겠죠.
아래 코드를 평가해봅시다.
>>> sub(pow(2, add(1, 10)), pow(2, 5))
2016
평가 절차(evaluation procedure)가 4번 적용되어야 합니다. 이를 시각화해보면 아래와 같은 계층 구조가 그려지네요.

해당 그림을 표현식 나무 또는 식 트리(expression tree)라고 부릅니다. 컴퓨터 과학에서 트리는 전통적으로 위에서 아래로 자라나는 형태를 가집니다. 각각의 지점에 해당하는 개체는 노드(node)라고 불리고, 이 경우에 노드는 표현식과 결과값들이 쌍을 맺고 있습니다(expressions pairred with their value).
Root(expression 전체)를 평가하는 작업은 이 식의 하위식인 브렌치들의 평가 결과가 필요하다. 단말 노드(leaf expression)의 식들은 함수나 식 둘다 될 수 있다(단말노드는 더이상 뿌리내릴게 없는 노드를 뜻함). 노드 내부(interior node)는 적용하기를 원하는 평가식(call expression which our evaluation rule is applied to)과 그 결과값(result of that expression)의 두 부분으로 나뉜다. 이 트리의 관점에서 평가 작업을 본다면 우리는 단말노드에서부터 피연산자들의 결과값이 여과되어 상위 계층에서 결합된다고 생각할 수 있다.(대충 위로 이동한다는 뜻인 것 같다)
첫번째 단계에서 호출식이 아닌 primitive expression을 보면, 다음과 같은 절차로 규정(stipulating)된다.
숫자 값은 숫자로 평가된다.
이름은 현재 환경과 연관된 값으로 평가된다.
environment의 중요한 역할이 식 안에서 기호의 의미를 결정하는 것이라는 사실에 집중해야한다.
add(x, 1)
x라는 이름에 대한 환경을 확인하지 않고 식을 평가하는 작업이 의미가 없다. 환경은 평가가 일어나는 맥락을 제공하기 때문에 우리가 프로그램 실행을 이해하는데 있어 중요한 역할을 한다.
이러한 평가 절차가 모든 Python code를 평가하기에 충분한 것은 아니다. 단지 이 절차는 호출식, 숫자, 이름을 평가하기 위한 것이다.
>>> x = 3할당문의 목적이 name에 값을 bind하는 것이기 때문에 실행 결과가 특정값을 리턴하지 않는다. 일반적으로 구문은 평가되지 않고 실행된다(not evaluated but executed). 실행과 값을 리턴하는 평가를 구분하라는 뜻인 것 같네요.
1.2.6 The Non-Pure Print Function
이 글을 통해 우리는 두가지 타입의 함수를 구분할 것이다
- 순수 함수(pure function)
input(argument)를 받아서 output을 리턴하는 함수
the built-in function
>>> abs(-2)
2인풋을 받아 아웃풋을 생산하는 작은 기계로 묘사될 수 있다.

abs()함수는 pure function이다. pure function은 값을 리턴하는 것 이상의 효과는 없다는 속성을 가진다. Pure function은 똑같은 argument에 대해 두 번 호출되었다면 똑같은 값을 리턴해야 한다.
- 비-순수 함수(Non-pure function)
순수 함수와 달리, 값을 리턴하는 것에 더해 부수 효과(side effect)를 만든다.
부수 효과란 interpreter나 컴퓨터의 상태를 변화시키는 것을 의미한다. 일반적인 부수 효과는 값을 리턴하는 것을 넘어 추가적인 아웃풋을 발생시킨다. print() 함수가 그 예시다.
>>> print(1, 2, 3)
123print() 함수와 abs 함수가 비슷해 보일 수 있지만 동작하는 방식은 근본적으로 다르다. print() 함수가 리턴하는 값은 항상 None인데, 이 None은 nothing을 의미하는 특별한 파이썬 값이다. <<코드잇에서도 수강했던 내용이죠? print() 함수의 경우에 호출됐을 때 output을 출력하는 부수 효과를 일으킨다.

>>> print(print(1), print(2))
1
2
None Noneprint()가 None을 리턴한다는 것의 의미는 할당문의 대상이 될 수 없다는 의미다.
>>> two = print(2) #할당문 사용
2 #print()가 display하는 2, 하지만 two에 저장값은 None
>>> print(two)
Nonepure function은 부수효과를 만들어내거나 행위가 변경되지 않는다는 제약이 있다. 이런 제약을 두는 것에서 오는 장점도 있는데, 첫 번째는 pure function이 안정적인 합성 호출식으로 결합될 수 있다는 점이다. 위에서 non-pure function인 print()가 피연산자로 사용되면 제대로 된 결과를 볼 수 없음을 보았다. 하지만 max나 pow, sqrt등은 중첩식으로 사용될 때 효과적일 수 있다.
두 번째, pure function은 테스트 하기 쉽다. argument만 동일하다면 항상 같은 값을 리턴하기 때문에 expected return value와 비교해봄으로써 잘 작동하는지를 쉽게 확인할 수 있다.
세 번째, pure function은 동시성 프로그래밍(concurrent programming)을 위해서는 필수적이라는 것이다. 동시성 프로그래밍은 동시에 실행되는 호출식들을 의미한다.
Ch. 1.3
숫자와 산술 연산(arithmetic operations)이 이미 정의된 원시 타입(primitive built-in)과 함수여야 한다.
Nested function application이 연산들의 조합을 의미하도록 설계되어 있어야 한다.
값에 이름을 할당하는 것이 제한된 의미의 추상화를 제공해야 한다.
이제부터 함수의 정의(function definition)에 대해 알아볼 것이다. 이는 unit이라고 부를 수 있는 복합 연산에 이름을 부여하는 좀 더 강력한 추상화 기술이다.
제곱(squaring)이라는 개념을 어떻게 표현하는지를 살펴보는 것으로부터 시작하자.
def square(x):
return mul(x, x)
어떻게 선언하면 square라는 이름의 새로운 함수를 정의한 것이다. 이 사용자 정의 함수(user-defined function)는 interpreter에 내장된 함수가 아니다. 이 함수는 자기자신을 한 번 곱하는 연산을 표현하고 있다. 여기서 x는 형식 파라미터(formal parameter)라고 부르며, 이는 제곱되어지는 요소에 대한 이름을 제공한다. 이 정의는 사용자 정의 함수를 생성하고 square라는 이름을 그 정의에 연관시킨다.
[함수를 어떻게 정의하는가?]
이 함수의 정의는 <name>을 가리키는 def 구문과 <formal parameter>를 가리키는 쉼표로 구분된 리스트, 그리고 함수의 몸통(function body)에 해당하는 return 구문으로 구성된다.
def <name> (<formal parameters>):
return <return expression>두번째 라인은 들여쓰기가 되어야한다. 대부분 space 4개를 indent로 사용한다. 그리고 return 구문은 즉시 evaluate되지는 않는다. 이는 새롭게 정의된 함수의 일부로써 저장되어 있다가 최종적으로 적용될 때 evaluate된다.
이렇게 함수를 적용하고나면 호출 표현(call expression)으로 square를 사용할 수 있다.
>>> square(21)
441
>>> square(add(2, 5))
49
>>> square(square(3))
81물론 이 square 함수를 다른 함수 정의를 위한 building block으로 사용할 수도 있다. 예를 들어, 다음처럼 sum_square 함수를 정의하여 두 함수의 제곱을 더하는 함수도 만들 수 있다.
def sum_squares(x, y):
return add(square(x), square(y))>>> sum_squares(3, 4)
25사용자 정의 함수도 built-in 함수가 사용되는 방식과 똑같은 방법으로 사용한다. sum_squares 함수가 interpreter에 내장되어 있는지, 다른 모듈로부터 import한건지, 사용자가 직접 정의한 것인지를 interpreter가 말해줄 수는 없다.
def 구문과 할당문은 둘다 값에 이름을 부여하기 때문에, 한 가지가 수행되면 이전까지 존재하던 binding은 전부 사라진다. 예를 들어, 아래 g()는 원래 argument가 없는 함수를 가리키다가, 숫자가 되었다가, argument가 2개인 함수가 된다.
>>> def g():
return 1
>>> g()
1
>>> g = 2
>>> g
2
>>> def g(h, i):
return h+i
>>> g(1, 2)
3
1.3.1 Environments
형식 파라미터가 내장 함수의 이름과 같다면, 2개의 함수 이름을 혼동 없이 공유할 수 있을까? 이런 의문을 해소하기 위해 environments에 대해 더 자세히 알아볼 필요가 있다.
Environments는 일종의 메모리 공간이고, 식의 평가가 이루어지는 공간이다. 환경은 프레임의 순서(sequence of frame)로 구성되어 있다. 각각의 frame은 binding을 포함하고, 이 binding은 name과 그에 상응하는 값의 연관이 있다. 우선 import문에 의해서 pi가 환경의 첫 번째 frame에 더해진다. 2번 라인의 할당문이 수행되면 tau가 global frame에 더해진다.
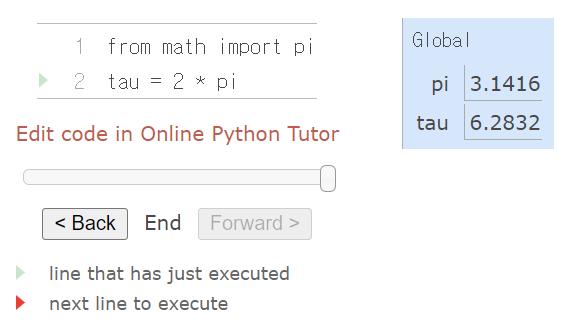
함수의 선언 또한 environment diagram에 나타난다. import문이 built-in function의 이름에 대한 binding을 보여줬다면 def문은 사용자 정의 함수를 정의함으로써 생성된 함수에 name을 binding한다.

각각의 함수 라인은 func로 시작해서 함수의 이름과 형식 파라미터가 열거된다. mul과 같은 built-in function 같은 경우에는 형식 파라미터(x등) 이름이 없고 항상 '...'가 사용된다.
함수의 이름은 2번 반복되는데, frame에서 한 번 사용되고 함수 자체가 나타나는 부분에서도 사용된다. 함수 안에서 등장하는 이름을 intrinsic name이라고 칭하고, frame에 나오는 이름을 bound name이라고 칭한다. 이 둘의 차이는 여러 다른 이름들이 하나의 같은 함수를 참조할 수는 있지만 함수 자체가 가지는 intrinsic name은 하나일 수 밖에 없다는 것이다.
Function Signatures
함수는 받아들이는 arguments의 개수에 따라 달라진다. 위에 나온 사용자 정의 함수 square는 x만을 argument로 받는다. 둘 이상의 argument를 호출식에서 넘긴다면 오류가 뜰 것이다. 형식 파라미터를 서술하는 내용을 function signature라고 한다.
1.3.2 Calling User-Defined Function
사용자가 정의한 함수의 호출식을 평가할 때, 인터프리터는 계산적인 프로세스(computational process)를 따른다. 어떤 호출식이든 인터프리터는 operator와 operand 식을 평가하고 이를 해당하는 이름의 함수에 적용한다.
사용자 정의 함수를 적용하는데 있어서 local frame이라는 개념을 짚고 넘어가자. local frame은 딱 그 함수에서만 접근할 수 있는 frame이다. global frame과 범위에서 차이가 난다고 할 수 있겠다. 몇개의 arguments를 가지고 사용자 정의 함수를 적용하는 과정은 다음과 같다.
- 새로운 local frame 안에 함수의 형식 파라미터 이름과 arguments의 이름을 bind한다.
- 이 frame에서 시작하여 해당하는 environment에서 함수의 body를 실행한다.
함수의 body가 실행되는 environment는 2개의 frame으로 구성되는데, 첫 번째는 형식 파라미터 바인딩을 가지고 있는 local frame이고, 두 번째는 모든 것을 다 가지고 있는 global frame이다. 각각의 함수 어플리케이션 인스턴스들은 독자적인 local frame을 가지고 있다.
처음에는 mul이라는 이름만이 global frame에 담긴다.

두 번째 라인을 실행했을 때, square 함수의 정의문이 실행된다. 3번 라인까지 진행되는건 직관적으로 이해할 수 있을 것이다. 함수를 정의했으니, square 함수도 global frame에 담긴다.

그 다음엔 4번 구문을 실행하면서 square 함수가 argument -2로 호출된다. 그렇게 형식 파라미터 x가 -2에 바운드되어 새로 생성된 frame에 담긴다.

x라는 이름이 현재 environment에 생기면서 크게 두 프레임으로 나뉘게 되었다. square(-2)에 의해 함수 내부가 실행되어 3번 구문이 실행되고, 결과값 4가 return된다.

해당 예문에서는 2개의 다른 environment가 사용되었다. square(-2)는 top-level expression이고 global environment에서 실행되었다. 하지만 이 함수 안에 있는 return mul(x, x)는 square를 호출함으로써 생겨난 environment(파란 박스)에서 평가되었다. 여기서 x와 mul은 같은 environment에서 바운드 되었지만, 속한 frame은 달랐다.
environment 안에서의 frame들간의 순서는 식에 이름을 찾을 때 return되는 값에 영향을 미친다. 직관적으로 받아들일 수 있는 것 같다.
Name Evaluation
name은 그 이름이 있는 environment의 최신 frame에서 값에 할당된다. ???
environment의 개념적인 틀과 이름들, 함수들이 평가 모델을 구성한다.
1.3.3 Example: Calling a User-Defined Function
사용자 정의 함수의 호출식이 평가되는 과정을 살펴보자



이후 8번 줄에서, global frame 안에서 사용자 정의 함수에 binding된 sum_squares라는 이름을 평가한다. 원시 숫자식(primitive numeric expressions)인 5와 12도 함께 평가된다.
그 다음, 5, 12를 각각 x, y에 bind해서 sum_squares에 적용한다.
그런데, sum_squares의 body는 다음 호출식을 포함하고 있다.

3개의 보조식(subexpressions)들은 sum_squares라고 이름이 붙여진 현재의 environment에서 평가된다.
operator subexpression인 add는 global frame에서 발견되는 이름으로, 덧셈을 위한 built-in function에 바인딩되어 있다. 그 다음 차례로 평가되는 2개의 operand subexpression은 덧셈이 적용되기 이전에 평가된다. 이 두 operands는 sum_squares라는 frame이 시작됨가 동시에 현재의 environment(파란 박스)에서 평가된다.
그림에서 operand 0의 경우, square라는 이름은 global frame에 있는 사용자 정의 함수의 이름이다. 2번 줄에서, sqaure라는 사용자 정의 함수를 정의내렸다. 반면 x는 local frame에 있는 5라는 숫자 값이다. 파이썬은 local frame의 5를 x에 바인딩한 후에 이를 square에 적용한다.
이 environment에서는 식 mul(x, x)가 25로 평가된다. 마찬가지로, operand 1의 경우도 y에 12를 bind하고 square를 적용한다. operand 1은 144로 평가된다.


마지막으로 argument인 25와 144에 덧셈을 적용하여 sum_squares 의 최종 리턴값은 169가 된다.

name들은 독립적인 local frame들에 흩어져있는 값들에 바인드된다. 다만 하나의 global frame에는 공유되는 이름들이 있다. 함수가 호출될 때마다 새로운 local frame이 생성되며, 같은 함수가 2번 호출되어도 따로 local frame이 생성된다.
이러한 메커니즘은 프로그램의 실행 중에 이름들을 적절한 시점에 적절한 값에 할당(resolve)하는 것을 보장하기 위해 존재한다. 3개의 local frame(sum_squares, square, square) 전부는 x라는 이름에 대한 바인딩을 가지고 있다. 같은 x 이름을 쓰고 있지만, 각각 다른 frame에서 다른 값에 바인딩 되어 있다. local frame은 이 이름들을 분리해서 유지한다.
1.3.4 Local Names
함수를 구현하는데 있어서 함수의 행위(function's behavior)에 영향을 주지 않는 것 한 가지는 함수의 형식 파라미터들의 이름 선택이다.
>>> def square(x):
return mul(x, x)
>>> def square(y):
return mul(y, y)
파라미터 이름은 함수의 구현부(body)에서 계속 local로 유지되어야 한다. 이는 직관적으로 이해할 수 있는데, 파라미터들이 개별 함수들에 대해서 local이 아니라면, 위 예시에서 x 파라미터를 3개의 함수에서 동일한 이름으로 사용했을 때 혼동될 수 있다. 중요한 점은, 이름이 같더라도 다른 local frame에 있다면, 이 변수들은 서로 관계가 없다는 점이다. 컴퓨터 모델(model of computation)은 이 독립성을 유지하기 위해 설계되었다.
결론은, local name의 범위는 그 이름이 정의된 사용자 정의 함수의 body로 한정된다는 것이다. 이런 범위 동작(scope behavior)는 environment가 어떻게 동작하는지를 알려주는 중요 요소이다.
1.3.5 Choosing Names
이름의 교환성(interchangeability)은 형식 파라미터의 이름을 결정하는 것이 중요하지 않다는 것을 의미하는 내용이 아니다. 반대로, 잘 선택된 함수와 파라미터 이름은 사람이 함수 정의를 해석하는데 있어서 필수적이다.
아래는 코드를 작성하는데 있어서 적용되는 컨벤션이다.
- 함수 이름은 소문자이며, 단어가 underscore(_)로 구분된다.
- 함수의 이름은 일반적으로 인터프리터가 arguments에 적용하는 연산을 떠올리게 한다. (add, print, square)
- 파라미터 이름은 소문자이며, underscore_로 단어를 구분한다.
- 파라미터 이름은 해당 파라미터가 어떤 역할을 하는지 떠올리게 하도록 짓는 것이 좋다.
- 단일 문자(single letter)로 이름을 지정한 파라미터는 그 역할이 명확할 때만 허용된다. 추가적으로, l(소문자 엘), O(대문자 오), I(대문자 아이)등은 숫자(numerals)와 혼동되기 때문에 피해야 한다.
이 가이드라인도 많은 예외가 있다는 점을 참고하자.
1.3.6 Functions as Abstractions
위에서 정의내렸던 sum_squares는 간단했지만, 강력한 사용자 정의 함수의 전형적인 예시다. sum_square 함수는 square 함수의 관점에서 정의되었지만, square 함수의 input과 ouput이 갖는 관계에만 의존하고 있다.
덕분에 우리는 숫자를 어떻게 제곱할 것인지에는 신경쓰지 않고 sum_square 함수를 작성할 수 있었다. square 함수가 내부적으로 어떻게 계산되는지는 숨겨져 있는 상태였고, 이는 나중에 고려할 수 있었다. sum_squares에 대해서 고민하는 한은 square는 특정 함수의 body가 아닌 함수의 추상화된 형태(abstraction of function)으로서 호출된다는 뜻이다. 이 수준의 추상화 단계에서 square를 계산하는 함수는 어떤 것이든지 동일하게 좋다.
그렇기에 우리는 단순히 이 함수가 return 하는 값에만 신경을 쓰면서 두 함수의 결과값에 연산을 수행하면 된다.
Aspects of a functional abstraction (중요한 것 같지 않다)
함수적 추상화(functional abstraction)을 마스터하는데 있어서 3가지 핵심 속성을 이해하는 것이 중요하다. Domain이라는 용어는 함수가 받아들일 수 있는 arguments 집합을 의미한다. 함수의 범위(the range of a function)는 함수가 리턴할 수 있는 값의 집합이다. 함수의 의도(intent)는 input과 output이 계산되는 관계이다. 여기에는 이 계산으로부터 발생하는 부수효과(side effect)도 포함된다. Domain, range, intent의 관점에서 함수적 추상화를 이해하는 것은 복잡한 프로그램에서 함수를 올바르게 사용하는데 있어 필수적이다.
sum_squares를 구현할 때 사용했던 square 함수는 아래 3가지 속성을 가진다.
- domain은 하나의 실수이다.
- range는 양의 실수이다. (제곱한 것이 리턴값이니 당연하다)
- intent는 input을 제곱해서 output으로 리턴하는 것이다.
1.3.7 Operators
수학적인 연산자는 결합하는 방법을 제공하는 첫 번째 예시이다. 하지만 우리는 아직 이 연산자(operator)들이 식을 어떻게 평가하는지를 정의하지는 않았다.
중위 연산자(infix operator)를 사용하는 파이썬 식(expression)은 각각이 고유의 평가 절차를 가지고 있다. 하지만 이런 평가 절차들은 종종 호출식으로 대체된다. 예를 들면
>>> 2 + 3
5이런 덧셈식은 다음 호출식으로 대체된다.
>>> add(2, 3)
5중위 표기법(infix notation)은 호출식처럼 중첩될 수 있다.
>>> 2 + 3 * 4 + 5
19위 코드는 아래 코드와 동일한 결과값을 보인다.
>>> add(add(2, mul(3, 4)), 5)
19
이처럼 호출식을 중첩하는 것은 연산자 버전에 비해 더 명시적일지 몰라도 읽기는 힘들다. 파이썬은 또한 괄호를 사용한 subexpression도 허용하며, 이는 선행 규칙을 적용함으로써 중첩식의 구조를 좀 더 명시적으로 만든다.
>>> (2 + 3) * ( 4 + 5)
45이는 다음 식과 동일한 결과값을 보인다.
>>> mul(add(2,3), add(4,5))
45
나눗셈의 경우에, 파이썬은 2개의 infix notation을 제공한다. /와 //인데, /는 일반적인 나눗셈 연산으로 floating point(실수) 또는 decimal value를 리턴한다. float과 decimal은 숫자를 표현하는데 있어서 차이가 있지만, 일단은 그냥 넘어가자. 결론만 말하면 float 타입은 2진 부동소수점으로 숫자를 표현하는데, decimal은 10진 소수점 숫자를 정확하게 표현한다는게 그 차이다.
>>> 5 / 4
1.25
>>> 8 / 4
2.0
//를 사용하면 결과값을 정수로 내림한다.
>>> 5 // 4
1
>>> -5 // 4
-2
이 두 연산자는 truediv와 floordiv 함수로 대체 가능하다.
>>> from operator import truediv, floordiv
>>> truediv(5, 4)
1.25
>>> floordiv(5, 4)
1
파이썬에서는 간단한 수학 연산에 대해서 이 함수 호출보다는 연산자를 사용하는 것이 더 자연스럽다(idomatic).
Ch. 1.4
1.4.1 Documentation
함수를 정의할 때는 해당 함수가 어떤 작업을 수행하는지 설명하는 docstring(문서)을 포함시켜야한다. 이 docstring은 함수의 body에 들여쓰기해서 작성되어지며, 쌍따옴표 3개(""")로 감싼다. Docstring의 첫 문장에는 해당 함수가 어떤 일을 하는지 요약 정리한다.
▶A function definition will often include documentation describing the function, called a docstring, which must be indented along with the function body. Docstrings are conventionally triple quoted("""). The first line describes the job of the function in one line.
>>> def pressure(v, t, n):
"""Compute the pressure in pascals of an ideal gas.
Applies the ideal gas law: http://en.wikipedia.org/wiki/Ideal_gas_law
v -- volume of gas, in cubic meters
t -- absolute temperature in degrees kelvin
n -- particles of gas
"""
k = 1.38e-23 # Boltzmann's constant
return n * k * t / v
추후에 help()를 사용해서 해당 함수의 docstring을 확인할 수 있다. help() argument 자리에 함수명을 넣으면 된다.
그럼, 이 """와 #의 차이는 뭘까? #은 help() 명령어를 통해 호출해도 나타나지 않는다. # 코멘트는 인터프리터에 의해서 철저히 무시되기 때문이다. #는 오로지 인간을 위해서 존재한다는 점을 기억하자.
1.4.2 Default Argument Values
함수를 작성할 때 추가로 argument를 넣을 수 있지만, 인자 수가 너무 많게 되면 함수를 호출하는데도 힘들어지고 코드를 읽기도 어려워진다.
파이썬 함수에서는 함수 인자에 default값을 optional로 넣을 수 있다.
>>> def pressure(v, t, n=6.022e23):
"""Compute the pressure in pascals of an ideal gas.
v -- volume of gas, in cubic meters
t -- absolute temperature in degrees kelvin
n -- particles of gas (default: one mole)
"""
k = 1.38e-23 # Boltzmann's constant
return n * k * t / v위 코드에서는 n값을 default값으로 지정했다.
>>> pressure(1, 273.15)
2269.974834
>>> pressure(1, 273.15, 3 * 6.022e23)
6809.924502
첫 번째 줄에서는 n값을 따로 지정하지 않아서, 함수에 내장되어 있는 n의 default값이 사용된 결과값이 출력되었다.
▶The pressure function is defined to take three arguments, but only two are provided in the first call expression above. In this case, the value for n is taken from the def statement default.
세 번째 줄에서는 n자리에 새로운 값을 할당하였고, 이에 따라 다른 출력값이 나온걸 확인할 수 있다.
▶If a third argument is provided, the default is ignored.
Ch. 1.5
제어문은 논리적 비교의 결과에 따라 프로그램의 실행 흐름을 제어하는 구문입니다. 제어문은 value(값)을 가지지 않고, 무언가를 계산하는 대신에 인터프리터가 다음에 수행해야할 작업을 결정하는 역할을 한다.
1.5.1 Statements
여태 우리는 세가지 종류의 statement들:assignment, def, return에 대해 다루어봤었죠. 이 파이썬 코드줄들은 각각 expression을 구성 요소로 포함하고 있지만, 이 코드줄 자체는 expression이 아닙니다.
statement는 평가되는 것이 아니라 실행됩니다. return문과 assignment에서 보았듯이, statement를 실행할 때는 statement내에 포함된 subexpressions들을 평가할 수 있습니다.
▶As we have seen for return and assignment statements, executing statements can involve evaluating subexpressions contained within them.
Expressions들도 statement처럼 실행될 수 있는데, evaluate되면 그 값은 버려지게 됩니다. Pure function을 실행하면 아무 효과가 없지만, non-pure function을 실행하면 함수 실행의 결과로 효과가 발생할 수 있습니다.
▶Expressions can also be executed as statements, in which case they are evaluated, but their value is discarded.
>>> def square(x):
mul(x, x) # Watch out! This call doesn't return a value.해당 함수는 리턴 값이 없어서 호출하여도 결과값이 없다.
Expression의 결과값을 만들어내고 싶다면, 할당문을 사용하거나 return문을 사용하면 될 것이다.
>>> def square(x):
return mul(x, x)
1.5.2 Compound Statements
파이썬 코드는 문장의 연속으로 이루어집니다. 단순 문장은 콜론(:)으로 끝나지 않는 한 줄입니다.
▶In general, Python code is a sequence of statements. A simple statement is a single line that doesn't end in a colon.
복합 문장은 다른 문장들(단순과 복합)으로 구성되어 있습니다. 복합 문장은 일반적으로 여러 줄에 걸쳐있고, 문장의 시자근 콜론으로 끝나는 한 줄 짜리 헤더로 시작합니다.
▶A compound statement is so called because it is composed of other statements (simple and compound). Compound statements typically span multiple lines and start with a one-line header ending in a colon, which identifies the type of statement
헤더와 들여쓰기된 문장 모음을 통틀어서 절(clause)이라고 부릅니다. 복합 문장은 하나 이상의 절로 구성됩니다.
▶A compound statement consists of one or more clauses
<header>:
<statement>
<statement>
...
<separating header>:
<statement>
<statement>
...
Simple statements:
Expressions, return statements, assignment statements
Compound statement:
def statement
각 헤더 유형에 대한 specialized evaluation 규칙이 헤더의 코드 블록(suite)이 실행되는 시점과 여부를 결정하는데, 이를 헤더가 블록을 제어한다고 표현합니다(The header control its suite).
예를 들어, def문에서는 return expression이 즉시 평가되지 않고, 정의된 함수가 나중에 호출되었을 때 사용 가능하도록 저장됩니다.
▶In the case of def statements, we saw that the return expression is not evaluated immediately, but instead stored for later use when the defined function is eventually called.
Sequence는 첫 번째 요소와 나머지 요소들로 분해할 수 있다. 문장들의 sequence의 나머지 부분은 다시 문장들의 sequence가 된다. 이 실행 규칙은 재귀적으로 적용할 수 있다.
▶A sequence can be decomposed into its first element and the rest of its elements. The "rest" of a sequence of statements is itself a sequence of statements!
1.5.3 Defining Functions II: Local Assignment
본래 사용자 정의 함수의 몸통 부분은 single return expression으로 작성된 단일 return문으로 구성되어 있었다고 설명했었습니다. 하지만 사실, 함수는 single expression을 넘어서 sequence of operations(일련 연산)로 정의할 수도 있습니다.
사용자 정의 함수가 적용될 때마다, 해당 함수에 포함된 일렬 연산절이 local environment에서 실행됩니다. 이 로컬 환경은 함수 호출에 의해 생성된 local frame으로 시작되는 환경을 말합니다. Return문은 제어 흐름을 변경하는 역할을 하는데, 첫 번째 return문이 시행되면 함수 적용 과정이 종료되며, return expression의 값이 곧 함수의 반환값이 됩니다.
def percent_difference(x, y):
difference = abs(x-y)
return 100 * difference / x
result = percent_difference(40, 50)
할당문의 효과는 현재 환경의 첫 번째 프레임에서 name을 값에 bind하는 것입니다. 즉, 함수 몸통 내에 존재하는 할당문은 global frame에 아무런 영향을 끼치지 못하는 거죠. 함수가 오직 로컬 환경에서만 작업할 수 있다는 사실은 모듈식 프로그램(modular programs)를 만드는데 중요하며, 이러한 프로그램에서 pure function은 입력과 반환값을 통해서만 상호 작용합니다.
1.5.4 Conditional Statements
파이썬은 절댓값(absolute values)를 계산하기 위한 내장 함수를 가지고 있습니다. 바로 abs()죠.
>>> abs(-2)
2
이번 챕터에서는 if문을 배워볼겁니다. 아래에서 우리가 보일 예시는 x가 양수라면, abs(x) 함수가 x를 리턴하고, 음수일 경우에는 0을 리턴하며, 둘다 아닐 경우에는, -x를 반환하는 함수입니다. 이러한 함수는 조건문을 사용해서 만들어야합니다.
def absolute_value(x):
"""Compute abs(x)."""
if x > 0:
return x
elif x == 0:
return 0
else:
return -x
result = absolute_value(-2)
조건문(conditional statements):
파이썬에서의 조건문은 headers 시리즈와 suites로 구성되는데: if절(clause)은 필수, elif절과 else절은 선택 사항입니다.
if <expression>:
<suite>
elif <expression>:
<suite>
else:
<suite>조건문을 시행하면, 각 clause는 순서대로 고려됩니다. 계산 과정은 다음과 같습니다.
1. Header expression을 평가한다.
2. 만약 if문이 참이면, 해당 suite을 시행합니다.. 그리고, 다음 순서에 오는 모든 clauses들을 전부 스킵합니다.
3. 만약 if와 elif를 거쳐 else절에 도달하게 되면, 해당 else절이 시행된다. (if와 elif가 전부 false 값으로 평가된거겠죠?)
불린 맥락(Boolean contexts):
위에서의 실행 절차는 "False 값"과 "True 값"을 언급했었습니다.
조건 블록의 header문 안에 있는 표현식은 불린 맥락에 있다고 말합니다.
▶ The expressions inside the header statements of conditional blocks are said to be in boolean contexts.
이 표현식의 참/거짓 값이 제어 흐름(control flow)에 영향을 주지만, 그렇지 않으면 해당 값이 할당되거나 반환되지 않습니다. Python에는 0, None, 그리고 불린값 False를 포함한 여러 가지 False값이 존재합니다. 그 외의 모든 숫자는 True값입니다. 2장에서 우리는 Python의 모든 내장 데이터 유형(built-in kind of data)이 참값과 거짓값을 가진다는 것을 알게 될 것입니다.
불린 값(Boolean values):
파이썬은 두 불린값을 가지고 있는데, 이는 True와 False입니다. 불린값은 논리적 표현식(logical expressions)에서 truth값을 나타내는데, 내장 비교연산자(built-in comparison operations)들이 불린값을 반환합니다.
논리 연산자(comparison operations):
- >
- <
- >= (operator module 의 ge 함수)
- <=
- == (operator module 의 eq 함수)
- !=
불린 연산자(Boolean operators):
세 개의 기초 논리 연산자도 파이썬에 내장되어 있습니다.
>>> True and False
False
>>> True or False
True
>>> not False
True
논리적 표현식은 그에 대응하는 평가 절차를 가지고 있습니다. 이러한 절차는 논리적 표현식의 참/거짓 값을 모든 하위 표현식을 평가하지 않고도 결정할 수 있는 경우를 활용하는데, 이를 단락 평가(short-circuiting)라고 합니다.
<left> and <right> 표현식을 평가하려면:
- 하위 표현식 <left>를 평가합니다.
- 결과가 거짓 값 v라면, 전체 표현식은 v로 평가됩니다.
- 그렇지 않다면, 표현식은 하위 표현식 <right>의 값으로 평가됩니다.
<left> or <right> 표현식을 평가하려면:
- 하위 표현식 <left>를 평가합니다.
- 결과가 참 값 v라면, 전체 표현식은 v로 평가됩니다.
- 그렇지 않다면, 표현식은 하위 표현식 <right>의 값으로 평가됩니다.
not <exp> 표현식을 평가하려면:
- <exp>를 평가합니다. 결과가 거짓 값이라면 True로, 그렇지 않으면 False로 평가됩니다. (반대로 바꿔주기)
이러한 값, 규칙, 연산자를 통해 우리는 비교 연산자를 활용할 수 있습니다. 비교를 수행하고 불린 값을 반환하는 함수는 보통 is로 시작하며, underscore(_) 없이 바로 뒤에 명칭이 옵니다(ex: isfinite, isdigit, isinstance 등).
1.5.5 Iteration
제어문은 어떤 구문을 실행할지 고르는 것 외에도 반복을 표현하는데 사용됩니다. 만약 우리가 작성한 코드의 각 줄이 단 한 번만 실행된다면, 프로그래밍은 매우 비생산적인 작업이 될 것입니다. 대신 명령문을 이용해 특정 구문을 반복적으로 실행하면 더욱 효율적이겠죠. 우리는 앞서 이미 반복의 한 형태를 보았습니다. 함수는 딱 한 번만 정의되지만 여러 번 호출될 수 있습니다. 반복 제어 구조(iterative control structures)는 같은 명령문을 여러 번 실행하기 위한 또 다른 메커니즘입니다.
피보나치 수열(Fibonacci numbers)을 생각해봅시다. 이 수열에서의 각 숫자는 앞의 두 숫자를 더한 값입니다.
0, 1, 1, 2, 3, 5, 8, 13, 21, ...
각 값은 앞의 두 숫자를 더하는 규칙을 반복적으로 적용하여 만들어집니다. 첫 번째와 두 번째 숫자는 각각 0과 1로 고정됩니다. 예를 들어, 여덟 번째 피보나치 수는 13입니다.
우리는 while문을 사용하여 n개의 피보나치 수를 나열할 수 있습니다. 생성한 값의 개수(k), k번째 값(curr), 그리고 그 이전 값(perdecessor)(pred)을 추적해야 합니다. 이 함수를 단계별로 따라가면서 피보나치 수가 하나씩 생성되는 과정을 살펴보겠습니다. 생성된 값은 curr에 bound됩니다.
def fib(n):
"""Compute the nth Fibonacci number, for n >= 2."""
pred, curr = 0, 1 # Fibonacci numbers 1 and 2
k = 2 # Which Fib number is curr?
while k < n:
pred, curr = curr, pred + curr
k = k + 1
return curr
1result = fib(8)
할당문에서 쉼표는 여러 이름과 값을 구분한다는 점을 기억합시다.
pred, curr = curr, pred + curr
이 문구는 pred라는 이름을 curr의 값으로 리바인딩하고 동시에 curr을 pred + curr의 값으로 리바인딩하고 있습니다.
= 오른쪽의 모든 표현식은 어떤 리바인딩이던간 제일 먼저 평가됩니다.
왼쪽의 어떤 바인딩을 업데이트하기 전에 = 오른쪽의 모든 것을 평가하는 것은 이 함수의 정확도를 위해 필수적입니다.
while 절은 헤더 표현식(header expression)과 그 뒤에 오는 문(suite)으로 구성됩니다:
while <expression>:
<suite>while 절을 실행하려면:
- 헤더 표현식을 평가합니다.
- 만약 참 값이라면, suite을 실행한 후 1단계로 돌아갑니다.
2단계에서는 while 절의 전체 문(entire suite)이 실행된 후 헤더 표현식이 다시 평가됩니다.
while문이 무한히 실행되는 것을 방지하기 위해, 각 반복마다 항상 어떤 바인딩 값이 변경되어야 합니다.
종료되지 않는 while 문을 무한 루프(infitie loop)라고 합니다. Python이 루프를 중단하도록 강제하려면 <Ctrll>-C를 누르면 됩니다.
1.5.6 Testing
함수를 테스팅하는 것은 해당 함수의 동작이 기대와 일치하는지를 검증하는 행위입니다. 현재 함수의 언어는 충분히 복잡해져서 구현을 테스트하기 시작해야 합니다.
테스트는 이 검증을 체계적으로 수행하기 위한 메커니즘입니다. 테스트는 일반적으로 테스트할 함수에 대한 하나 이상의 샘플 호출을 포함하는 또 다른 함수의 형태를 취합니다. 그런 다음 반환된 값이 예상 결과와 비교되어 검증됩니다. 대부분의 함수는 일반적으로 사용되도록 설계된 반면, 테스트는 특정 인수 값을 가진 호출을 선택(selecting)하고 검증(validating)하는 것을 포함합니다. 테스트는 또한 문서화 역할(doocumentation)을 하며, 함수 호출 방법과 적절한 인수 값이 무엇인지 입증합니다.
단언(Assertions):
프로그래머들은 assert 문을 사용하여 기댓값을 검증합니다. 예를 들어, 테스트 중인 함수의 출력과 기댓값이 같은 지를 검증합니다. assert 문은 불린 맥락의 표현식으로 구성되어 있으며, 그 뒤에는 표현식이 거짓 값으로 평가될 경우 표시될 인용된 텍스트(단일 또는 이중 따옴표 모두 사용 가능하지만 일관성을 유지해야 함)가 옵니다.
▶ An assert statement has an expression in a boolean context, followed by a quoted line of text (single or double quotes are both fine, but be consistent) that will be displayed if the expression evaluates to a false value.
>>> assert fib(8) == 13, 'The 8th Fibonacci number should be 13'
assert문이 참이라면, 아무런 결과도 나타나지 않지만 만약 시행을 멈추는 에러 현상이 발생한다면 그것은 assert문이 거짓이란 뜻입니다.
위 예시로 살펴봤던 피보나치 수열 함수를 테스팅 해보기 위해 몇개의 인자를 테스트해볼건데, 이때 인자엔 극히 큰 값도 포함할 것입니다.
>>> def fib_test():
assert fib(2) == 1, 'The 2nd Fibonacci number should be 1'
assert fib(3) == 1, 'The 3rd Fibonacci number should be 1'
assert fib(50) == 7778742049, 'Error at the 50th Fibonacci number'
Python 코드를 인터프리터에 직접 입력하는 대신 파일에 작성할 때, 테스트는 일반적으로 같은 파일이나 _test.py suffix가 있는 이웃 파일(neighboiring file)에 작성됩니다.
Doctests:
Python은 함수의 docstring에 간단한 테스트를 직접 삽입할 수 있는 편리한 방법을 제공합니다. Docstring의 첫 번째 줄에는 함수에 대한 한 줄 설명이 포함되어야 하며, 그 뒤에 빈 줄이 와야합니다. 인수(argument)와 동작(behavior)에 대한 자세한 설명이 뒤따를 수 있습니다. 또한, docstring에는 함수 호출을 포함한 샘플 상호 세션(sample interactive session)이 포함될 수 있습니다:
>>> def sum_naturals(n):
"""Return the sum of the first n natural numbers.
>>> sum_naturals(10)
55
>>> sum_naturals(100)
5050
"""
total, k = 0, 1
while k <= n:
total, k = total + k, k + 1
return total
이렇게, 상호작용은 doctest module을 통해 검증될 수 있습니다. 아래에 globals 함수는 global environment의 representation을 리턴합니다. 이건 인터프리터가 표현식을 평가하기 위해 필요한 것 입니다. 이해가 안간다
>>> from doctest import testmod
>>> testmod()
TestResults(failed=0, attempted=2)
단일 함수에 대한 docterst interaction을 검증하기 위해, run_docstring_examples라는 doctest 함수를 사용합니다. 이 함수는 (안타깝게도) 호출하는 데 다소 복잡합니다. 첫 번째 인자는 테스트할 함수입니다. 두 번째 인자는 항상 globals() 표현식의 결과값이여야 합니다. globals()함수는 global environments을 반환하는 내장 함수입니다. 세 번째 인자는 "verbose" 출력을 원한다는 것을 나타내기 위해 True로 설정합니다. 즉, 실행된 모든 테스트의 목록(catalog)을 제공합니다.
>>> from doctest import run_docstring_examples
>>> run_docstring_examples(sum_naturals, globals(), True)
Finding tests in NoName
Trying:
sum_naturals(10)
Expecting:
55
ok
Trying:
sum_naturals(100)
Expecting:
5050
ok
함수의 반환 값이 예상 결과와 일치하지 않을 때, run_docstring_examples 함수는 이 문제를 테스트 실패로 보고합니다.
Python 코드를 파일에 작성할 때, 파일에 있는 모든 doctest는 다음과 같이 doctest 명령줄 옵션(command line option)으로 Python을 시작하여 실행할 수 있습니다:
python3 -m doctest <python_source_file>효과적인 테스트의 핵심은 새로운 함수를 구현한 직후에 테스트를 작성하고 실행하는 것입니다. 어떤 예제 입력과 출력을 머릿속에 그리기 위해 구현 전에 일부 테스트를 작성하는 것도 좋은 연습입니다. 단일 함수를 적용하는 테스트를 단위 테스트(unit test)라고 합니다. 철저한 단위 테스트는 좋은 프로그램 설계의 특징입니다.
Ch. 1.6
이제까지 우리는 함수가 특정 인수값과 관계 없이 복합 연산(compound operations)을 설명하는 추상화의 방법임을 보았습니다. 예를 들어, square() 함수가 있었죠.
>>> def square(x):
return x * x>>> 3 * 3
9
>>> 5 * 5
25그리고 square()을 명시적으로 언급하지 않고도 작업할 수 있습니다. 이러한 방식은 제곱과 같은 간단한 계산에는 충분하지만, abs나 fib와 같은 더 복잡한 예제에서는 번거로워질 것입니다. 일반적으로 함수 정의가 없으면 항상 언어에서 기본 제공 연산(이 경우에는 곱셈)의 수준에서만 작업해야 하는 단점이 생깁니다. 결과적으로 프로그램은 제곱을 계산할 수는 있지만, 제곱이라는 개념을 표현하는 능력이 부족하게 됩니다.
강력한 프로그래밍 언어라면 공통 패턴에 이름을 붙여 추상화하고, 그 이름을 통해 직접 작업할 수 있는 능력을 제공해야 합니다. 함수는 이러한 능력을 제공합니다. 다음 예제에서 보듯, 코드에 자주 등장하는 공통 프로그래밍 패턴들이 여러 함수와 함께 사용됩니다. 이러한 패턴들 또한 우리가 직접 이름을 붙여서 추상화할 수 있습니다.
특정 일반 패턴을 이름 붙인 개념으로 표현하기 위해, 다른 함수를 인수로 받거나 함수를 값으로 리턴하는 함수를 만들어야 합니다. 함수를 다루는 함수를 고차 함수(higher-order function)라고 합니다. 이 장에서는 고차 함수가 강력한 추상화 메커니즘으로 어떻게 작용하는지 보여주며, 이로 인해 언어의 표현력을 크게 확장할 수 있음을 설명합니다.
>>> def sum_naturals(n):
total, k = 0, 1
while k <= n:
total, k = total + k, k + 1
return total
>>> sum_naturals(100)
5050>>> def sum_cubes(n):
total, k = 0, 1
while k <= n:
total, k = total + k*k*k, k + 1
return total
>>> sum_cubes(100)
25502500>>> def pi_sum(n):
total, k = 0, 1
while k <= n:
total, k = total + 8 / ((4*k-3) * (4*k-1)), k + 1
return total
>>> pi_sum(100)
3.1365926848388144위 세 함수는 분명하게 공통되는 기본 패턴을 공유하고 있습니다. 때문에 우리는 같은 템플릿에서 빈 칸을 채워 각각의 함수를 템플렛으로부터 생성할 수 있습니다.
def <name>(n):
total, k = 0, 1
while k <= n:
total, k = total + <term>(k), k + 1
return total
이러한 공통 패턴이 존재한다는 것은 추상화가 사용되기만을 기다리고 있다는 강력한 증거입니다. 각 함수는 항(term)들의 합을 계산하는 함수입니다. 프로그램 설계자로서 우리는 특정 합을 계산하는 함수뿐만 아니라, ‘합산(summation)’이라는 개념 자체를 표현하는 함수를 작성할 수 있는 강력한 언어를 원합니다. 파이썬에서는 위에 제시된 공통 템플릿을 사용하여 빈 칸을 형식 매개변수로 변환함으로써 쉽게 구현할 수 있습니다.
아래 예제에서 summation() 함수는 상한(upper bound) n과 k번째 항을 계산하는 함수 term(), 이렇게 두 가지를 인수로 받습니다. 우리는 summation() 함수를 다른 함수처럼 사용할 수 있으며, 이는 summation을 간결하게 표현합니다. 예제를 단계별로 살펴보면서, term이라는 local name에 cube를 결합하여 1∗1∗1 + 2∗2∗2 + 3∗3∗3 = 36의 결과가 올바르게 계산되는 것을 확인해봅시다.
def summation(n, term):
total, k = 0, 1
while k <= n:
total, k = total + term(k), k + 1
return total
def cube(x):
return x*x*x
def sum_cubes(n):
return summation(n, cube)
result = sum_cubes(3)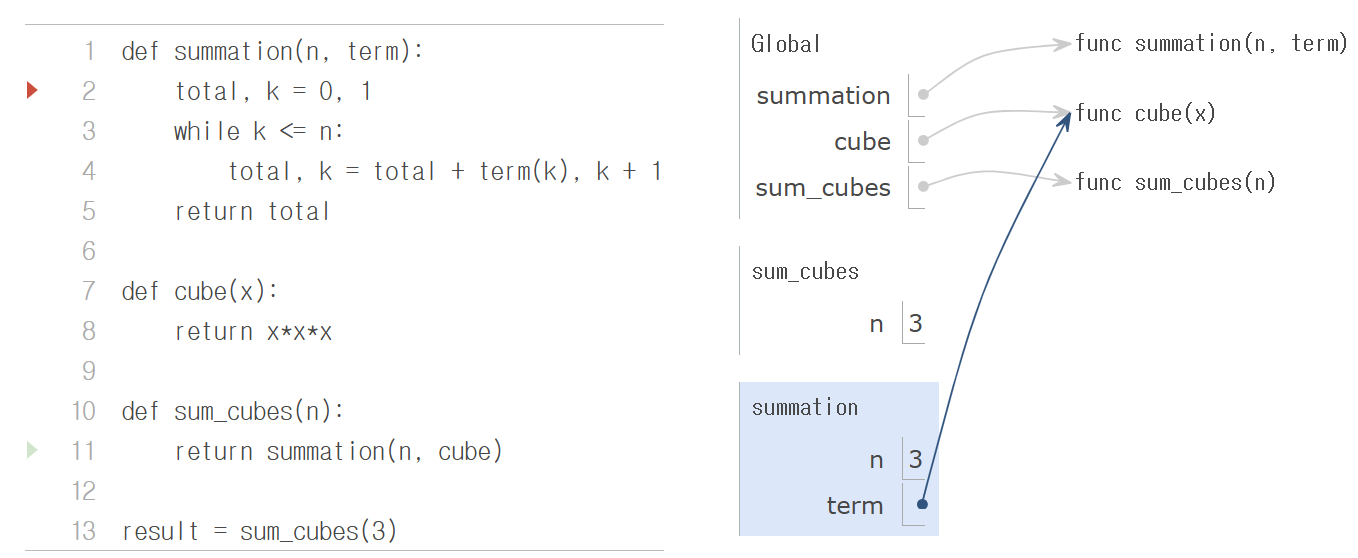
인수 값을 그대로 리턴하는 항등 함수 identity() 를 사용하여, summation 함수를 사용해 자연수의 합을 구했던 것과 같이 같은 결과를 얻을 수 있습니다. (이걸 왜 이렇게 하는거지..?)
>>> def summation(n, term):
total, k = 0, 1
while k <= n:
total, k = total + term(k), k + 1
return total
>>> def identity(x):
return x
>>> def sum_naturals(n):
return summation(n, identity)
>>> sum_naturals(10)
55summation() 함수는 특정 수열(sequence)을 위한 별도의 함수를 정의하지 않고도 직접 호출할 수 있습니다.
>>> summation(10, square)
385
π를 근사하는 pi_sum() 함수를 정의하기 위해 summation 추상화를 사용할 수 있으며, 각 항을 계산하는 함수 pi_term()을 정의하여 사용합니다. π에 가까운 값을 생성하기 위해 1e6(1 * 10^6 = 1000000의 약어)이라는 인수를 전달합니다.
>>> def pi_term(x):
return 8 / ((4*x-3) * (4*x-1))
>>> def pi_sum(n):
return summation(n, pi_term)
>>> pi_sum(1e6)
3.141592153589902사용자 정의 함수는 특정 숫자와 관계없이 수치 연산의 패턴을 추상화하는 메커니즘으로 도입되었습니다(언제든 원하는 숫자로 바꿔치기 할 수 있도록). 고차 함수(higher-order functions)를 통해 이제 더 강력한 추상화를 볼 수 있는데, 일부 함수는 호출하는 특정 함수와 무관하게 일반적인 계산 방법(general methods of computation)을 표현합니다.
함수의 의미에 대한 이러한 개념적 확장에도 불구하고, 호출 표현식을 평가하는 환경 모델은 고차 함수의 경우에도 변경 없이 자연스럽게 확장됩니다. 사용자 정의 함수가 인수에 적용되면, 새로운 지역 프레임(a new local frame)에서 형식 매개변수가 해당 인수의 값(함수일 수도 있는 값)에 바인딩됩니다.
다음은 반복적 개선을 위한 일반적인 방법을 구현하고, 이를 사용해 황금비를 계산하는 예입니다. 황금비는 "phi"라고도 불리며 자연, 예술, 건축에서 자주 나타나는 약 1.6에 가까운 숫자입니다.
반복적 개선 알고리즘은 방정식의 해에 대한 추정값(guess)으로 시작하며, 업데이트 함수(update function)를 반복적으로 적용해 추정값을 개선하고, 현재 추정값(current guess)이 "충분히 가까운지" 확인하는 비교를 적용합니다.
>>> def improve(update, close, guess=1):
while not close(guess):
guess = update(guess)
return guess이 improve 함수는 반복적 정제(repetitive refinement)를 일반적으로 표현합니다. 해결하려는 문제를 구체적으로 명시하지 않으며, 해당 세부 사항은 인수로 전달된 update와 close 함수에 맡깁니다.
▶This improve function is a general expression of repetitive refinement. It doesn't specify what problem is being solved: those details are left to the update and close functions passed in as arguments.
황금비의 잘 알려진 특성 중 하나는 어떤 양수의 역수에 1을 반복적으로 더하여 계산할 수 있으며, 이는 자신의 제곱보다 1만큼 작다는 것입니다. 이러한 특성을 improve와 함께 사용할 함수로 표현할 수 있습니다.
>>> def golden_update(guess):
return 1/guess + 1
>>> def square_close_to_successor(guess):
return approx_eq(guess * guess, guess + 1)>>> def approx_eq(x, y, tolerance=1e-15):
return abs(x - y) < tolerance>>> improve(golden_update, square_close_to_successor)
1.6180339887498951이 예시는 컴퓨터 과학의 두 가지 중요한 아이디어를 설명합니다. 첫째로, 이름과 함수를 통해 엄청난 복잡성을 추상화할 수 있습니다. 각 함수 정의는 단순하지만, 평가 절차에 의해 시작된 계산 과정은 상당히 복잡합니다. 둘째, Python 언어의 매우 일반적인 평가 절차 덕분에 작은 구성 요소들이 복합적인 과정으로 조합될 수 있습니다. 프로그램을 해석하는 절차를 이해하면 우리가 만든 과정을 검증하고 점검할 수 있습니다.
계속 우리가 다루어왔듯이, 새로 만든 general method improve의 정확성을 확인하기 위한 테스트가 필요합니다. 황금비는 정확한 폐쇄형 해(exact closed-form solution)를 가지고 있기 때문에, 이 반복적 결과와 비교해 테스트를 제공할 수 있습니다.
>>> from math import sqrt
>>> phi = 1/2 + sqrt(5)/2
>>> def improve_test():
approx_phi = improve(golden_update, square_close_to_successor)
assert approx_eq(phi, approx_phi), 'phi differs from its approximation'
>>> improve_test()위 예제들은 함수를 인수로 전달할 수 있는 기능이 프로그래밍 언어의 표현력을 얼마나 크게 향상시키는지 보여줍니다. 각 일반 개념이나 방정식은 고유한 짧은 함수로 매핑됩니다. 이 접근 방식의 부정적인 결과 중 하나는, 전역 프레임에 작은 함수들의 이름이 넘쳐나게 되는데(becomes cluttered) 이들 모두 고유한 이름을 가져야 한다는 점입니다. 또 다른 문제는 특정 함수 서명(particular function signatures)에 의해 제약된다는 것입니다. 예를 들어 improve의 update 인수는 정확히 하나의 인수만 받아야 합니다. 중첩 함수 정의(nested function definition)는 이러한 문제를 해결할 수 있지만, 환경 모델을 확장(enrich)해야 합니다.
새로운 문제를 생각해 봅시다: 숫자의 제곱근을 계산하는 것입니다. 프로그래밍 언어에서는 제곱근을 종종 sqrt로 줄여 표기합니다. 다음 코를 반복적으로 적용하면 a의 제곱근으로 수렴합니다.
>>> def average(x, y):
return (x + y)/2
>>> def sqrt_update(x, a):
return average(x, a/x)
이 두 개의 인수를 받는 update 함수는 improve와 호환(incompatible)되지 않으며, 단일 업데이트(single update)만 제공하여 반복적 업데이트(repeated updates)로 제곱근을 구해야 하는 요구 사항을 충족하지 않습니다. 이 문제들을 해결하는 방법은 함수 정의를 다른 함수의 정의 부 내부에 위치시키는 것입니다.
▶The solution to both of these issues is to place function definitions inside the body of other definitions.
>>> def sqrt(a):
def sqrt_update(x):
return average(x, a/x)
def sqrt_close(x):
return approx_eq(x * x, a)
return improve(sqrt_update, sqrt_close)지역 할당(local assignment)과 마찬가지로, local def statements도 현재의 지역 프레임(current local frame)에만 영향을 미칩니다. 이러한 함수들은 sqrt가 평가되는 동안에만 범위 내에 존재합니다. 평가 절차(evaluation procedure)와 일관되게, 이러한 local def 문은 sqrt가 호출될 때까지는 평가되지도 않습니다.
렉시컬 스코프(Lexical scope)
▶This discipline of sharing names among nested definitions is called lexical scoping.
지역에서 정의된 함수들(Locally defined functions)은 자신이 정의된 스코프 내의 이름 바인딩에도 접근할 수 있습니다. 위 예제에서 sqrt_update는 자신을 둘러싼 함수 sqrt의 형식 매개변수인 a를 참조합니다. 이러한 중첩된 정의들 간에 이름을 공유하는 방식을 렉시컬 스코핑이라 합니다. 중요한 점은 내부 함수(inner functions)가 호출된 위치가 아닌(not where they are called), 정의된 환경 내의 이름들에 접근할 수 있다는 것(but where they are defined)입니다.
렉시컬 스코핑을 지원하기 위해 환경 모델에 두 가지 확장이 필요합니다.
- 각 사용자 정의 함수(user-defined function)는 부모 환경(parent environment)을 가지며, 이는 함수가 정의된 환경을 의미합니다.
- 사용자 정의 함수가 호출되면, 해당 함수의 지역 프레임(local frame)은 부모 환경을 확장합니다.
이전에는 모든 함수가 global environment에서 정의되었기 때문에 모두 동일한 부모(global environment)를 가졌습니다. 그러나 sqrt의 처음 두 절(clause)을 평가할 때 Python은 지역 환경(local environment)과 연관된 함수들을 생성합니다.
>>> sqrt(256)
16.0
이 환경은 먼저 sqrt에 대한 지역 프레임을 추가하고, 그 후에 sqrt_update와 sqrt_close에 대한 def 문을 평가합니다.
def average(x, y):
return (x + y)/2
def improve(update, close, guess=1):
while not close(guess):
guess = update(guess)
return guess
def approx_eq(x, y, tolerance=1e-3):
return abs(x - y) < tolerance
def sqrt(a):
def sqrt_update(x):
return average(x, a/x)
def sqrt_close(x):
return approx_eq(x * x, a)
return improve(sqrt_update, sqrt_close)
result = sqrt(256)
함수 값에는 이제 부모(parent)라는 새로운 주석(annotation)이 추가됩니다. 이 주석은 앞으로 환경 다이어그램에 포함될 것입니다. 함수 값의 부모는 그 함수가 정의된 환경의 첫 번째 프레임입니다. 부모 주석이 없는 함수들은 전역 환경(global environment)에서 정의된 것입니다. 사용자가 정의한 함수가 호출될 때, 생성되는 프레임은 그 함수와 동일한 부모를 갖습니다.
이후에, 이름 sqrt_update는 새로 정의된 함수로 해석되며, 이 함수는 improve 함수에 인수로써 전달됩니다. improve 함수의 바디 부분에서는 초기 추정치(initial guess) x가 1인 경우, update 함수(여기서는 sqrt_update에 바인딩됨)를 적용해야 합니다. 이 최종 적용은 sqrt_update에 대해 새로운 환경을 생성하며, 이 환경에는 x만 포함된 로컬 프레임이 생기지만 부모 프레임인 sqrt에는 여전히 a에 대한 바인딩이 남아 있습니다.
이 평가 절차에서 가장 중요한 부분은 sqrt_update의 부모가 sqrt_update 호출로 생성된 프레임으로 전달되는 것입니다. 이 프레임은 [parent=f1]으로 주석이 추가됩니다.
확장된 환경(Extended Environments): 환경은 임의의 길이만큼 프레임 체인(chain of frames)을 가질 수 있으며, 항상 전역 프레임에서 끝납니다. 이전의 sqrt 예제에서는 환경이 최대 두 개의 프레임(로컬 프레임과 전역 프레임)으로 구성되었습니다. 하지만 중첩된 def 문(nested def statements)을 통해 다른 함수 내에 정의된 함수를 호출함으로써 더 긴 체인을 만들 수 있습니다. 이 경우 sqrt_update 호출의 환경은 세 개의 프레임으로 구성됩니다: 로컬 sqrt_update 프레임, sqrt_update가 정의된 sqrt 프레임(f1으로 라벨링됨), 그리고 전역 프레임(global frame)입니다.
sqrt_update 바디 부분에서 반환식은 프레임 체인을 따라 a의 값을 해석할 수 있습니다. 이름들을 보는데, 현재 환경에서 해당 이름에 바인딩된 첫 번째 값을 찾습니다. 파이썬은 먼저 sqrt_update 프레임을 확인하지만 a가 존재하지 않습니다. 그다음 부모 프레임인 f1을 확인하여 a가 256에 바인딩되어 있음을 발견합니다.
이로써 우리는 파이썬의 렉시컬 스코핑의 두 가지 주요 이점을 이해할 수 있습니다.
- 로컬 함수의 이름이 정의된 함수 외부의 이름과 충돌하지 않습니다. 로컬 함수 이름은 함수가 정의된 현재 로컬 환경에 바인딩되므로 전역 환경에 영향을 미치지 않습니다.
- 로컬 함수는 둘러싼 함수의 환경(enclosing function)에 접근할 수 있습니다. 이는 로컬 함수의 본문이 그 함수가 정의된 평가 환경을 확장하는 환경에서 평가되기 때문입니다.
sqrt_update 함수는 정의된 환경에서 참조된 a의 값을 포함합니다. 이렇게 정보를 "포함(enclose)"하기 때문에, 로컬로 정의된 함수는 클로저(closures)라고 불리기도 합니다.
1.6.4 Functions as Returned Values
반환값 자체가 함수인 함수를 생성함으로써, 프로그램에서 더욱 강력한 표현력을 얻을 수 있습니다. 렉시컬 스코핑을 사용하는 프로그래밍 언어의 중요한 특징 중 하나는, 로컬로 정의된 함수가 반환될 때도 부모 환경을 유지한다는 점입니다. 다음 예시는 이 기능의 유용성을 보여줄 겁니다.
여러 간단한 함수가 정의된 후에는 함수 합성(function composition)이 자연스러운 결합 방식이 됩니다. 즉, 두 함수 f(x)와 g(x)가 주어졌을 때, h(x) = f(g(x))와 같은 방식으로 정의하고 싶을 수 있습니다. 기존 도구를 사용해 함수 합성을 정의할 수 있습니다:
>>> def compose1(f, g):
def h(x):
return f(g(x))
return h
다음 예시를 한 번 볼까요?
def square(x):
return x * x
def successor(x):
return x + 1
def compose1(f, g):
def h(x):
return f(g(x))
return h
def f(x):
"""Never called."""
return -x
square_successor = compose1(square, successor)
result = square_successor(12)
compose1에서의 1은 합성된 함수들이 모두 단일 인수(single argument)를 받는다는 것을 나타내기 위한 것입니다. 이 명명 규칙(naming convention)은 인터프리터에 의해 강제되지 않으며, 단지 함수 이름의 일부일 뿐입니다.
이 시점에서, 환경 모델을 정확히 정의하려는 노력이 주는 이점을 보기 시작합니다. 함수들을 이런 방식으로 반환할 수 있는 능력을 설명하기 위해 환경 모델을 수정할 필요는 없습니다.
1.6.5 Example: Newton's Method
이 확장된 예제는 함수 반환값과 로컬 정의(local definition)가 어떻게 협력하여 일반적인 아이디어를 간결하게 표현할 수 있는지를 보여줍니다. 이제 우리는 머신 러닝, 과학 계산, 하드웨어 설계, 최적화 등에서 널리 사용되는 알고리즘을 구현할 것입니다.
뉴턴 메소드는 수학 함수의 반환값이 0이 되는 인자를 찾는 고전적인 반복 접근 방식입니다. 이러한 값들을 함수의 영점(zeros)이라고 부릅니다. 함수의 영점을 찾는 것은 종종 제곱근 계산과 같은 다른 관심 문제를 해결하는 것과 동일하다고 볼 수 있습니다.
진행하기 전에 동기 부여가 될 만한 한 가지 언급을 하자면, 우리는 제곱근을 계산할 수 있다는 사실을 당연하게 여길 수 있습니다. 파이썬뿐만 아니라, 스마트폰, 웹 브라우저, 계산기에서도 제곱근을 계산할 수 있습니다. 그러나 컴퓨터 과학을 배우는 과정에서 이러한 수치들이 어떻게 계산될 수 있는지를 이해하는 것은 중요한 부분이며, 여기서 소개하는 일반적인 접근 방식은 파이썬에 내장된 함수 이상의 광범위한 방정식들을 해결하는 데 적용될 수 있습니다.
뉴턴 메소드는 추정치를 점차 개선해 나가는 반복 개선 알고리즘입니다. 이 방법은 미분 가능한, 다시 말해 임의의 점에서 직선으로 근사할 수 있는 함수의 영점 추정치(guess of the zero)를 개선합니다. 뉴턴의 방법은 이러한 선형 근사(linear approximation)를 따라 함수의 영점을 찾습니다.
함수 f(x)의 그래프에서 점 (x, f(x))을 지나면서 해당 지점에서 f(x)의 곡선과 동일한 기울기를 가진 직선을 상상해 봅시다. 이러한 직선을 접선(tangent line)이라 부르며, 이 기울기를 x에서의 f의 도함수(derivative of f at x)라고 합니다.
이 직선의 기울기는 함수 값의 변화량(ratio of the change in function)과 함수 인자의 변화량(change in function argument) 간의 비율입니다. 따라서 x를 f(x)로부터 기울기로 나눈 값만큼 이동시키면 이 접선이 0과 만나는 인자 값을 찾을 수 있습니다.

newton_update 함수는 함수 f와 그 도함수 df를 사용하여, 접선을 따라 0으로 이동하는 계산 과정을 표현합니다.
>>> def newton_update(f, df):
def update(x):
return x - f(x) / df(x)
return update마지막으로, find_root 함수는 newton_update와 improve 알고리즘, 그리고 f(x)가 0에 가까운지 비교하는 조건을 이용해 정의할 수 있습니다.
>>> def find_zero(f, df):
def near_zero(x):
return approx_eq(f(x), 0)
return improve(newton_update(f, df), near_zero)
근 계산(computing roots): 뉴턴의 방법을 사용하면 임의의 차수(arbitrary degree) n의 근을 계산할 수 있습니다. n차 근은 x를 n번 곱하여 a가 되는 값입니다. 예를 들어,
- 64의 제곱근(2차 근)은 8입니다. The square (second) root of 64 is 8.
- 64의 세제곱근(3차 근)은 4입니다. The cube (third) root of 64 is 4.
- 64의 여섯제곱근(6차 근)은 2입니다. The sixth root of 64 is 2.
다음과 같은 관찰을 통해 뉴턴의 방법을 사용하여 근을 계산할 수 있습니다:
- 64의 제곱근(루트64)는 아래 식의 x와 같습니다.

이를 일반화해보면,

이 마지막 방정식의 영점을 찾을 수 있다면, n차 근을 계산할 수 있습니다. n이 2, 3, 6이고 a가 64인 경우의 곡선을 그래프로 그리면 이러한 관계를 시각화할 수 있습니다.

먼저, square_root를 구현하기 위해 함수 f와 그 도함수 df를 정의합니다.
>>> def square_root_newton(a):
def f(x):
return x * x - a
def df(x):
return 2 * x
return find_zero(f, df)
>>> square_root_newton(64)
8.0해당 식을 일반화하면, f(x)=x^n - a의 미분식을 df(x) = n * x^(n-1) 로 나타낼 수 있겠죠?
>>> def power(x, n):
"""Return x * x * x * ... * x for x repeated n times."""
product, k = 1, 0
while k < n:
product, k = product * x, k + 1
return product
>>> def nth_root_of_a(n, a):
def f(x):
return power(x, n) - a
def df(x):
return n * power(x, n-1)
return find_zero(f, df)
>>> nth_root_of_a(2, 64)
8.0
>>> nth_root_of_a(3, 64)
4.0
>>> nth_root_of_a(6, 64)
2.0이 계산에서 발생하는 근사 오차(approximation error)는 approx_eq의 허용 오차(tolerance)를 더 작은 숫자로 변경함으로써 줄일 수 있습니다.
뉴턴의 방법을 실험할 때, 항상 수렴하지는 않음을 유의해야 합니다. improve의 초기 추정값(initial guess)은 영점에 충분히 가까워야 하며, 함수에 대한 여러 조건들이 충족되어야 합니다. 이러한 단점에도 불구하고, 뉴턴의 방법은 미분 가능한 방정식을 푸는 강력한 일반 계산 방법입니다. 현대 컴퓨터에서는 로그와 큰 정수 나눗셈에 대해 이 기법의 변형을 사용하여 매우 빠른 알고리즘을 구현하고 있습니다.
1.6.6 Currying
고차 함수(higher-order fuction)를 사용하여 여러 인수를 받는 함수를 각각 하나의 인수만 받는 함수의 체인으로 변환할 수 있습니다. 구체적으로, 함수 f(x, y)가 주어졌을 때, g(x)(y)가 f(x, y)와 같다는 걸 보이는 함수 g를 정의할 수 있습니다. 여기서 g는 단일 인수 x를 받고, 또 다른 단일 인수 y를 받는 함수를 반환하는 고차 함수입니다.
▶A higher-order function that takes in a single argument x and returns another function that takes in a single argument y.
이러한 변환(transformation)을 커링(currying)이라고 합니다.
예로, pow 함수의 커링 버전을 다음과 같이 정의할 수 있습니다:
>>> def curried_pow(x):
def h(y):
return pow(x, y)
return h
>>> curried_pow(2)(3)
8
Haskell과 같은 일부 프로그래밍 언어에서는 단일 인수만 받는 함수만 허용하므로, 프로그래머는 여러 인수를 받는 모든 함수를 커링해야 합니다. 파이썬과 같은 더 일반적인 언어에서는 단일 인수만 받는 함수가 필요할 때 커링이 유용합니다. 예를 들어, map 패턴은 단일 인수를 받는 함수를 값의 연속(sequence of values)에 적용합니다. 이후 뒷 장에서 map 패턴의 더 일반적인 예시를 볼 것이지만, 현재는 다음과 같은 함수로 이 패턴을 구현할 수 있습니다:
>>> def map_to_range(start, end, f):
while start < end:
print(f(start))
start = start + 1map_to_range와 curried_pow를 사용하여 처음 10개의 2의 거듭제곱을 계산할 수 있습니다. 이를 위해 특별히 함수를 작성하지 않고도 다음과 같이 할 수 있습니다:
>>> map_to_range(0, 10, curried_pow(2))
1
2
4
8
16
32
64
128
256
512비슷하게, 같은 두 함수를 사용하여 다른 수의 거듭제곱을 계산할 수 있습니다. 커링을 사용하면, 계산하고자 하는 수마다 별도의 함수를 작성하지 않고도 거듭제곱을 구할 수 있습니다.
위 예제에서는 pow 함수를 커링하여 curried_pow를 얻었지만, 커링 변환을 자동화하는 함수와 이를 역변환하는 언커링(uncurrying) 함수도 정의할 수 있습니다:
>>> def curry2(f):
"""Return a curried version of the given two-argument function."""
def g(x):
def h(y):
return f(x, y)
return h
return g
>>> def uncurry2(g):
"""Return a two-argument version of the given curried function."""
def f(x, y):
return g(x)(y)
return f
>>> pow_curried = curry2(pow)
>>> pow_curried(2)(5)
32
>>> map_to_range(0, 10, pow_curried(2))
1
2
4
8
16
32
64
128
256
512curry2 함수는 두 인수 함수 f를 받아서 단일 인수 함수 g를 반환합니다. g에 인수 x를 적용하면 또 다른 단일 인수 함수 h를 반환합니다. h에 y를 적용하면 f(x, y)가 호출됩니다. 따라서 curry2(f)(x)(y)는 f(x, y)와 동등합니다. uncurry2 함수는 커링 변환을 역으로 바꾸어서(reverse), uncurry2(curry2(f))가 f와 동등하게 만듭니다.
>>> uncurry2(pow_curried)(2, 5)
32
1.6.7 Lambda Expressions
지금까지 새로운 함수를 정의할 때마다 이름을 붙여야 했습니다. 하지만 다른 종류의 표현식에서는 중간 값(intermediate values)을 이름에 연관시키지 않아도 됩니다. 예를 들어, a*b + c*d를 계산할 때, a*b나 c*d와 같은 하위 표현식에 이름을 붙일 필요 없이 전체 표현식을 계산할 수 있습니다. 파이썬에서는 람다(lambda) 표현식을 사용하여 즉석에서 이름 없는 함수 값(unnamed functions)을 생성할 수 있습니다. 람다 표현식은 단일 반환 표현식을 바디으로 갖는 함수를 평가합니다. 할당문과 제어문은 허용되지 않습니다.
>>> def compose1(f, g):
return lambda x: f(g(x))
람다 표현식의 구조를 영어 문장으로 설명하면 다음과 같습니다:
lambda x : f(g(x))
"A function that takes x and returns f(g(x))"람다 표현식의 결과는 람다 함수(lambda fuction)라고 불립니다. 본질적인(intrinsic) 이름이 없기 때문에 파이썬은 <lambda>로 표시하지만, 그 외에는 일반 함수처럼 동작합니다.
>>> s = lambda x: x * x
>>> s
<function <lambda> at 0xf3f490>
>>> s(12)
144환경 다이어그램에서도 람다 표현식의 결과는 함수로 표시되며, 그리스 문자 λ(람다)로 명명됩니다. compose 예제는 람다 표현식을 사용하여 매우 간결하게 표현할 수 있습니다.
일부 프로그래머들은 람다 표현식으로 만든 이름 없는 함수를 사용하는 것이 더 간결하고 직접적이라고 느낍니다. 그러나 복합적인 람다 표현식은 짧지만 가독성이 떨어지기 쉽습니다. 다음 정의는 정확하지만, 많은 프로그래머가 빠르게 이해하는 데 어려움을 겪습니다.
>>> compose1 = lambda f, g: lambda x: f(g(x))
일반적으로 파이썬 스타일에서는 람다 표현식을 사용할 때 명시적인 def 문을 선호하지만, 간단한 함수가 인수나 반환값으로 필요할 때도 람다 표현식을 허용합니다.
이러한 스타일 규칙은 지침일 뿐이므로 원하는 대로 프로그래밍할 수 있습니다. 하지만 프로그램을 작성할 때 언젠가 프로그램을 읽을 사람이 있음을 염두에 두어야 합니다. 프로그램을 더 이해하기 쉽게 만들 수 있다면, 그들에게 도움이 됩니다.람다(lambda)라는 용어는 초기 수학 표기법과 타자 시스템의 제한이 맞지 않아서 생긴 역사적 우연입니다.
Ch. 1.7
함수가 recursive 하다고 불리는 경우는, 직접적인이든 간접적이든 함수의 바디가 함수 자신을 호출할 때입니다. recusive 함수의 바디를 실행하는 과정은 그 함수를 다시 적용하도록 요구하는 것일 수도 있다는 거죠. 파이썬에서 recursive 함수는 어느 special syntax도 사용하지 않습니다.
예시 문제를 먼저 살펴볼건데요. natural number(자연수)의 digit을 합하는 함수를 작성해봅시다. recursive function을 만들 때, 문제가 더 단순한 문제들로 쪼개질 수 있는 방법이 있는지 먼저 찾아봐야합니다. 이 경우엔, 연산자 %와 // 가 숫자를 분리하는데 사용되죠: last digit과 last digit을 제외한 다른 digit들로 말이죠.
>>> 18117 % 10
7
>>> 18117 // 10
1811
자연수 18117 digit의 합은 18입니다. 숫자를 1, 8, 1, 1, 7로 분리할 수 있듯이, 이 숫자들의 합을 last digit인 7과 나머지 digit의 합인 1+8+1+1 = 11로 나눌 수 있죠. 이 분리 과정은 우리에게 알고리즘을 보여주고 있습니다. 숫자 n의 digit의 합을 구하기 위해선, last digit인 n % 10을 남은 숫자인 n // 10에서의 digit 합에 더해야 하는거죠. 한 가지 특수한 경우가 있다면, 주어진 숫자 n이 한자리 수 one digit일 경우, n의 sum of digit은 n 그 자체가 됩니다. 이 알고리즘은 recursive function으로 시행될 수 있어요.
>>> def sum_digits(n):
"""Return the sum of the digits of positive integer n."""
if n < 10:
return n
else:
all_but_last, last = n // 10, n % 10
return sum_digits(all_but_last) + last
sum_digit 함수의 정의는 완성되었고, 오류가 없습니다. sum_digit 함수가 자신의 body안에서 호출되고 있음에도 말이죠. 숫자 n의 digit을 합하는 과정은 두 스텝으로 나뉩니다. last digit을 제외한 모든 자리를 더하고, last digit을 더해주는거죠. 이 두 스텝은 오리지널 문제보다 더 간단합니다. 이 함수가 recursive하다고 불리는 이유는 첫번째 스텝이 오리지널 문제와 같은 유형의 문제기 때문입니다. sum_digit 함수를 시행하기 위해 필요한 함수는 그 자신 자체인 sum_digit 함수인거죠,
>>> sum_digits(9)
9
>>> sum_digits(18117)
18
>>> sum_digits(9437184)
36
>>> sum_digits(11408855402054064613470328848384)
126
환경 다이어그램을 통해 recursive 함수가 어떻게 적용되는지 이해하는 시간을 가져보겠습니다

def문이 실행되면, 이름 sum_digits가 새로운 함수에 연결되지만, 해당 함수의 본문은 아직 실행되지 않습니다. 따라서 sum_digits의 순환적 성격(circular nature)은 아직 문제가 되지 않습니다. 이후 8번 라인으로 인해 sum_digits가 738로 호출됩니다:
1. sum_digits 의 지역 프레임이 생성되며, 이 프레임에서 n은 738에 바인딩됩니다. 이후 함수 본문이 이 프레임으로 시작되는 환경에서 실행됩니다.
2. 738이 10보다 작지 않으므로 4번째 줄의 할당문이 실행되어 738이 73과 8로 나뉩니다.
3. 이어지는 return 문에서, 현재 환경에서 all_but_last의 값인 73으로 sum_digits 가 다시 호출됩니다.
4. sum_digits 의 새로운 지역 프레임이 생성되며, 이번에는 n이 73에 바인딩됩니다. 함수 본문은 이 새로운 프레임으로 시작되는 환경에서 다시 실행됩니다.
5. 73 또한 10보다 작지 않으므로, 73이 7과 3으로 나뉘고, 이번에는 all_but_last의 값인 7로 sum_digits가 호출됩니다.
sum_digits 의 세 번째 지역 프레임이 생성되며, 이번에는 n이 7에 바인딩됩니다.
6. 이 프레임으로 시작되는 환경에서 n < 10이 참이므로 7이 반환됩니다.
7. 두 번째 지역 프레임에서 이 반환값 7은 last 값인 3과 합산되어 10을 반환합니다.
8. 첫 번째 지역 프레임에서 이 반환값 10은 last 값인 8과 합산되어 최종적으로 18을 반환합니다.
이 재귀 함수는 순환적 특성(circular character)에도 불구하고 올바르게 작동합니다. 이는 각 호출이 이전보다 더 단순한 문제를 처리하기 때문입니다. 또한, 두 번째 호출은 첫 번째 호출보다 더 단순한 문제를 다루고 있었습니다.
sum_digits(18117) 호출에 대한 환경 다이어그램을 생성하면, 각 후속 호출이 이전 호출보다 작은 인수를 사용하며, 결국 한 자리 숫자(single-digit input)에 도달하는 것을 확인할 수 있습니다.
이 예시는 단순한 본문을 가진 함수가 재귀를 통해 복잡한 계산 과정을 어떻게 발전시킬 수 있는지를 보여줍니다.
1.7.1 The Anatomy of Recursive Functions (재귀 함수의 구조)
많은 재귀 함수의 본문에서 공통적인 패턴을 발견할 수 있습니다. 함수의 바디는 기본 사례(base case)로 시작하며, 이는 가장 단순한 입력에 대한 함수의 동작을 정의하는 조건문입니다. sum_digits의 경우, 베이스 케이스는 한 자리 숫자 인수이며, 이 경우 단순히 해당 인수를 반환합니다. 일부 재귀 함수는 여러 베이스 케이스를 가질 수 있습니다.
기본 사례 뒤에는 하나 이상의 재귀 호출(recursive calls)이 이어집니다. 재귀 호출은 항상 원래 문제를 단순화하는 특성을 가지고 있습니다. 재귀 함수는 문제를 점진적으로 단순화하면서 계산을 표현합니다. 예를 들어, 7의 자릿수 합을 계산하는 것은 73의 자릿수 합을 계산하는 것보다 더 간단하며, 이는 다시 738의 자릿수 합을 계산하는 것보다 간단합니다. 각 후속 호출마다 남은 작업량은 점점 줄어듭니다.
재귀 함수는 종종 우리가 이전에 사용한 반복적 접근 방식(iterative approaches)과는 다른 방식으로 문제를 해결합니다. 예를 들어, n 팩토리얼을 계산하는 fact 함수( fact(4) = 4! = 4⋅3⋅2⋅1 = 24 )를 고려해봅시다.
while 문을 사용한 자연스러운 구현은 n까지의 양의 정수를 모두 곱하여 결과를 누적합니다.
>>> def fact_iter(n):
total, k = 1, 1
while k <= n:
total, k = total * k, k + 1
return total
>>> fact_iter(4)
24
반면, 팩토리얼 함수의 재귀적 구현(recursive implementation)은 fact(n)을 더 단순하게 fact(n-1)로 표현할 수 있습니다. 재귀의 베이스 케이스는 문제의 가장 단순한 형태입니다. 예를 들어, fact(1) 이 1의 값을 가지는 것처럼요.

이 두 팩토리얼 함수는 개념적으로 다릅니다. 반복적 함수(iterative function)는 1이라는 베이스 케이스에서 시작해 각 항(term)을 순차적으로 곱해 최종 결과를 만들어냅니다. 반면에, 재귀적 함수(recursive function)는 최종 항인 n과 더 단순한 문제인 fact(n-1)의 결과를 사용해 직접 결과를 구성합니다.
재귀 호출(recursion)이 fact함수의 연속적인 적용으로 점점 더 단순한 문제를 처리하면서 "풀려(unwinds)" 나가면, 결국 베이스 케이스에서부터 결과가 구축됩니다. 재귀는 1을 fact에 전달하면서 끝나며, 각 호출의 결과는 다음 호출에 의존하다가 기본 사례에 도달하면 종료됩니다.
이 재귀 함수의 정확성은 팩토리얼의 수학적 정의에서 쉽게 검증할 수 있습니다:
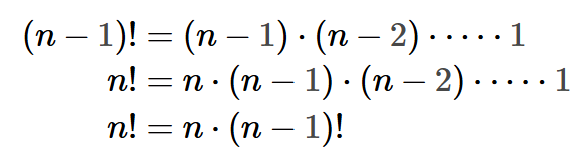
우리가 계산 모델을 사용해 재귀를 풀어낼 수도 있지만, 재귀 호출을 함수적 추상화(fucntional abstraction)로 생각하는 것이 종종 더 명확합니다. 즉, fact 바디 부분에서 fact(n-1)이 어떻게 구현되었는지 신경 쓰지 말고, 단순히 그것이 (n−1)!를 올바르게 계산한다고 믿어야 합니다. 이런 접근법을 "재귀적 신뢰의 도약(recursive leap of faith)"이라고 부릅니다. 우리는 함수를 정의하지만(?), 더 단순한 사례들이 올바르게 작동할 것이라고 신뢰하면서 함수의 정확성을 검증합니다. 이 예시에서는 fact(n-1)이 (n−1)!를 올바르게 계산한다고 가정하고, 이 가정이 맞을 때 n!가 올바르게 계산되는지만 확인하면 됩니다. 이런 방식으로 재귀 함수의 정확성을 검증하는 것은 귀납법(proof of induction)에 의한 증명과 유사합니다.
fact_iter 함와 fact 함수는 또 다른 차이점이 있습니다. 전자(fact_iter)는 total과 k라는 두 가지 추가 이름을 도입해야 하지만, 재귀 구현(recursive implementation)에서는 필요하지 않습니다. 일반적으로 반복적 함수(iterative functions)는 계산 과정에서 변하는 로컬 상태(local state)를 유지해야 합니다. 반복 과정의 어느 시점이든, 그 상태는 완료된 작업의 결과와 남은 작업량을 나타냅니다. 예를 들어, k가 3이고 total이 2일 때, 처리해야 할 항은 아직 3과 4가 남아 있습니다. 반면에, fact는 단일 인수 n으로만 표현됩니다. 계산 상태는 전적으로 환경 구조 안에 포함되며, 반환 값이 total의 역할을 하고, n은 각 프레임에서 다른 값에 바인딩됩니다. 따라서 k를 명시적으로 추적할 필요가 없습니다.
재귀 함수는 호출 표현식(call expression)을 평가하는 규칙을 활용해 이름을 값에 바인딩하며, 반복 중 로컬 이름을 올바르게 할당하는 번거로움을 피하는 경우가 많습니다. 이러한 이유로 재귀 함수는 올바르게 정의하기가 더 쉬울 수 있습니다. 그러나 재귀 함수가 만들어내는 계산 과정을 이해하려면 연습이 필요합니다.
1.7.2 Mutual Recursion
두 함수가 서로를 호출하며 재귀적 절차를 나누어 수행할 때, 이러한 함수들을 **상호 재귀적 함수(mutually recursive functions)**라고 합니다. 예를 들어, 다음과 같은 음수가 아닌 정수의 짝수(even)와 홀수(odd)에 대한 정의를 고려해 보세요:
1. 어떤 숫자가 짝수라는 것은 그것이 한 홀수보다 1만큼 크다는 의미입니다.
2. 어떤 숫자가 홀수라는 것은 그것이 한 짝수보다 1만큼 크다는 의미입니다.
3. 0은 짝수입니다.
이 정의를 사용하여 숫자가 짝수인지 홀수인지 판단하는 상호 재귀적 함수를 구현할 수 있습니다:

상호 재귀적 함수는 하나의 재귀 함수로 변환할 수 있습니다. 이는 두 함수 사이의 추상 경계(abstraction boundary)를 제거하고, is_odd의 바디 내용을 is_even에 통합하는 방식으로 가능합니다. 예를 들어: n을 is_odd 바디에 n-1로 대체하여 넣어서 인자를 전달하는 것이죠.
>>> def is_even(n):
if n == 0:
return True
else:
if (n-1) == 0:
return False
else:
return is_even((n-1)-1)이처럼 상호 재귀는 단순한 재귀보다 신비롭거나 강력하지 않습니다. 그러나 복잡한 재귀적 프로그램에서 추상화를 유지하는 메커니즘을 제공합니다.
1.7.3 Printing in Recursive Functions
재귀 함수가 진화시키는 계산 과정을 종종 print 호출을 사용하여 시각화할 수 있습니다. 예를 들어, 가장 큰 숫자부터 가장 작은 숫자까지, 그리고 다시 가장 큰 숫자로 숫자의 모든 접두(prefix)를 출력하는 cascade 함수를 구현해 보겠습니다.
>>> def cascade(n):
"""Print a cascade of prefixes of n."""
if n < 10:
print(n)
else:
print(n)
cascade(n//10)
print(n)
>>> cascade(2013)
2013
201
20
2
20
201
2013이 재귀 함수에서 기본 사례(base case)는 한 자릿수 숫자로, 이를 출력합니다. 그렇지 않은 경우, 재귀 호출은 두 개의 print 호출 사이에 위치합니다.
베이스 케이가 재귀 호출보다 먼저 표현될 필요는 없습니다. 실제로, 조건문에서 print(n)이 반복된다는 점을 관찰하면 더 간결하게 표현할 수 있습니다.
>>> def cascade(n):
"""Print a cascade of prefixes of n."""
print(n)
if n >= 10:
cascade(n//10)
print(n)다음으로, 두 명의 플레이어가 참여하는 게임을 고려해 보겠습니다. 초기 상태에서 테이블 위에는 n개의 돌(pebbles)이 있습니다. 플레이어들은 번갈아 가며 1개 또는 2개의 돌을 제거할 수 있으며, 마지막 돌을 제거하는 플레이어가 승리합니다.
Alice와 Bob이 게임을 한다고 가정하고, 아래와 같은 전략을 사용한다고 가정합시다:
1. Alice는 항상 돌 1개를 제거합니다.
2. Bob은 짝수 개의 돌이 남아 있으면 2개를 제거하고, 그렇지 않으면 1개를 제거합니다.
초기 돌의 개수가 n개이고 Alice가 먼저 시작할 때, 누가 승리할까요?
이 문제를 해결하기 위해 각 전략을 별도의 함수로 캡슐화할 수 있습니다. 이를 통해 하나의 전략을 변경하더라도 다른 전략에 영향을 미치지 않고 추상화 경계를 유지할 수 있습니다. 게임의 턴제 특성(turn by turn)을 구현하기 위해, 두 함수는 각 턴의 끝에서 서로를 호출합니다.
>>> def play_alice(n):
if n == 0:
print("Bob wins!")
else:
play_bob(n-1)
>>> def play_bob(n):
if n == 0:
print("Alice wins!")
elif is_even(n):
play_alice(n-2)
else:
play_alice(n-1)
>>> play_alice(20)
Bob wins!play_bob 함수에서는 여러 재귀 호출이 포함될 수 있습니다. 그러나 이 예제에서는 play_bob의 각 호출이 play_alice를 최대 한 번만 호출합니다. 다음 섹션에서는 단일 함수 호출이 여러 개의 직접 재귀 호출을 수행할 때 발생하는 상황을 살펴봅니다.
1.7.4 Tree Recursion
다른 일반적인 계산 패턴으로 **트리 재귀(tree recursion)**가 있습니다. 이는 함수가 자신을 두 번 이상 호출하는 경우를 말합니다. 예를 들어, 피보나치 수열(Fibonacci numbers)을 계산하는 문제를 생각해 봅시다. 피보나치 수열에서 각 숫자는 앞의 두 숫자의 합입니다.
def fib(n):
if n == 1:
return 0
if n == 2:
return 1
else:
return fib(n-2) + fib(n-1)
result = fib(6)
트리 재귀의 특징
이 재귀 정의는 피보나치 수열의 친숙한 정의를 정확히 반영하므로 매우 직관적입니다. 함수가 여러 번 재귀 호출을 수행하면 이를 트리 재귀(tree recursive)라고 합니다. 이는 각 호출이 여러 작은 호출로 분기되고, 각 작은 호출이 또 더 작은 호출로 분기되기 때문입니다. 이러한 과정은 나무의 가지가 줄기에서 뻗어 나가며 점점 더 작고 많아지는 모습과 유사합니다.
효율성 비교
우리는 이미 트리 재귀 없이 피보나치 수를 계산하는 함수를 정의할 수 있었습니다. 실제로, 이전의 시도는 계산 효율성 면에서 더 나았습니다(이 주제는 이후에 자세히 다룹니다). 그러나 이제 반복(iterative) 접근 방식보다 트리 재귀 솔루션이 훨씬 간단한 문제를 고려해 보겠습니다.
1.7.5 Example: Partitions
양의 정수 n을 최대 크기 m의 부분(part)을 사용하여 분할하는 경우의 수는 n을 m 이하의 양의 정수 부분으로 표현하는 방법의 수를 의미합니다. 각 표현은 크기가 점점 커지는 순서로 정렬됩니다. 예를 들어, 6을 최대 크기 4의 부분으로 분할하는 경우의 수는 9입니다.
6 = 2 + 4
6 = 1 + 1 + 4
6 = 3 + 3
6 = 1 + 2 + 3
6 = 1 + 1 + 1 + 3
6 = 2 + 2 + 2
6 = 1 + 1 + 2 + 2
6 = 1 + 1 + 1 + 1 + 2
6 = 1 + 1 + 1 + 1 + 1 + 1재귀 함수 정의
count_partitions(n, m) 함수는 최대 m 크기의 부분을 사용하여 n을 분할하는 서로 다른 경우의 수를 반환합니다. 이 함수는 다음과 같은 관찰을 기반으로 트리 재귀(tree recursion)를 사용하여 간단하게 정의할 수 있습니다:
n을 최대 크기 m의 정수를 사용해 분할하는 경우의 수는:
1. n−m을 최대 크기 m의 정수를 사용해 분할하는 경우의 수
2. n을 최대 크기 m−1의 정수를 사용해 분할하는 경우의 수
이것이 성립하는 이유는 n을 분할하는 모든 방법을 두 그룹으로 나눌 수 있기 때문입니다:
m을 포함하는 분할 / m을 포함하지 않는 분할.
첫 번째 그룹의 각 분할은 n−m의 분할에 m을 추가한 형태입니다. 위 예에서, 첫 번째와 두 번째 분할은 4를 포함하며, 나머지 분할은 그렇지 않습니다.
따라서 n을 최대 크기 m의 정수로 분할하는 문제를 두 가지 더 간단한 문제로 재귀적으로 나눌 수 있습니다:
1. 더 작은 숫자인 n−m을 분할.
2. 더 작은 구성 요소인 m−1까지를 사용한 분할.
코드를 작성하기 위해선 다음 베이스 케이스를 정의해야 합니다:
1. n=0인 경우, 분할 방법은 하나뿐입니다(부분을 포함하지 않음).
2. n<0인 경우, 분할 방법은 없습니다.
3. m≤0이고 n>0인 경우, 분할 방법은 없습니다.
>>> def count_partitions(n, m):
"""최대 크기 m의 부분을 사용해 n을 분할하는 방법의 수를 계산합니다."""
if n == 0:
return 1
elif n < 0:
return 0
elif m == 0:
return 0
else:
return count_partitions(n-m, m) + count_partitions(n, m-1)
>>> count_partitions(6, 4)
9
>>> count_partitions(5, 5)
7
>>> count_partitions(10, 10)
42
>>> count_partitions(15, 15)
176
>>> count_partitions(20, 20)
627
트리 재귀의 관점
트리 재귀 함수는 다양한 가능성을 탐색하는 방식으로 작동한다고 볼 수 있습니다. 이 경우, m 크기의 부분을 사용하는 경우와 사용하지 않는 경우를 탐색합니다. 첫 번째 재귀 호출과 두 번째 재귀 호출은 각각 이러한 가능성에 해당합니다.
이 함수를 재귀 없이 구현하는 것은 훨씬 더 복잡합니다. 관심 있는 독자들은 시도해 보길 권장합니다.
Works Cited
https://blog.naver.com/jwyoon25/221967147066
1.3 새로운 함수 정의하기
원제: Defining New Functions 이전 chapter에서 강력한 프로그래밍 언어라면 가지고 있어야 하는 몇 가...
blog.naver.com
https://blog.naver.com/jwyoon25/221802255026
1.1 시작
컴퓨터 과학은 엄청나게 넓은 학문적 훈련이다. 여기서 말하는 학문적인 영역은 전 세계적으로 분산된 시스...
blog.naver.com
https://dsaint31.tistory.com/514
[Python] Expression vs. Statement
Expression (표현식) 프로그래밍 또는 컴퓨터 과학 분야에서 Expression은 흔히, function call, identifier, number, operator, literal 등으로 이루어진다. 표현식(or 수식) 으로 번역. 하나의 value로 reduce 될 수 있는 c
dsaint31.tistory.com